計算問題は考え方を覚えれば確実に解けます。
第7問 解答・解説
No.7
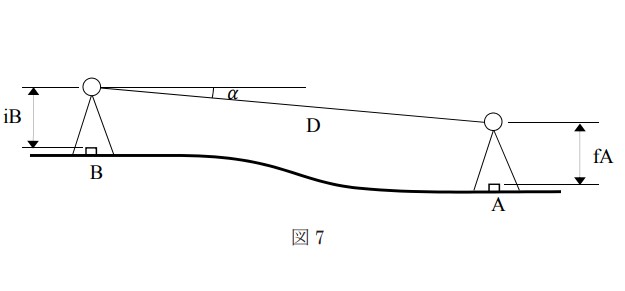
図7に示すとおり、新点Aの標高を求めるため、既知点Bから新点Aに対して高低角α及び斜距離Dの観測を行い、表7の結果を得た。新点Aの標高は幾らか。最も近いものを次の中から選べ。
ただし、既知点Bの器械高iBは1.40 m、新点Aの目標高fAは1.60 m、既知点Bの標高は350.00 m、両差は0.10 mとする。また、斜距離Dは気象補正、器械定数補正及び反射鏡定数補正が行われているものとする。
| α | -3°00’00” |
| D | 950.00m |
選択肢
１．297.38 m
２．300.08 m
３．300.18 m
４．300.38 m
５．303.38 m
第7問 解答・解説
正解は選択肢３です。
与えられた条件を図に書き込みました。解き方を考えてみましょう。
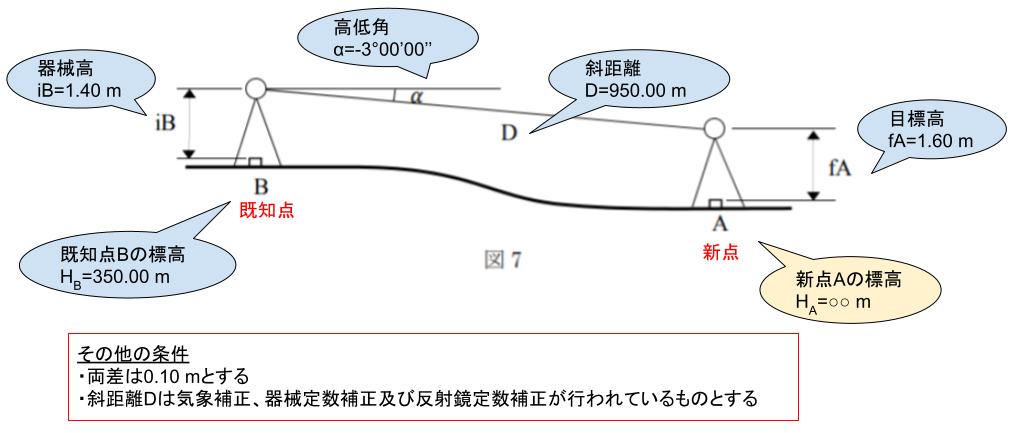
それでは解き方を解説します。
基本的には足し算、引き算をすることで答えを導くことができます。
注意すべきは「両差」の扱いです。
両差：（球差-気差）のこと。補正係数と思ってもらえれば良いです。
既地点から新点の観測を行う場合は足し算、新点から既知点の観測を行う場合は引き算にて計算します。
今回の問題では既知点から新点の観測なので足し算してあげればOKです。
計算問題は何回も解いて解き方を覚えちゃいましょう。
選択肢のうち答えに最も近いのは「選択肢3. 300.18 m」です。
以上！正解は選択肢３です。
補足：なぜsinを使うのか？
この問題で求めたい「高低差」が、観測によってできた直角三角形のどの辺に当たるかを確認することが、サインを使う理由になります。
1. 測量における直角三角形
観測点B、目標点A、そしてBの鉛直角（高低角）を基準にした水平線によって、下図のような直角三角形ができます。
| 記号 | 測量における意味 | 直角三角形での位置 |
| 斜距離 D | トータルステーションで観測した距離 | 斜辺（一番長い辺） |
| 高低角 α | 水平線となす角度 | 角度 |
| 高低差 h | 求める高さ（垂直距離） | 対辺（αの向かいの辺） |
2. サイン（sin）の定義
三角関数は、直角三角形の2辺の比で定義されます。サインは、斜辺に対する対辺の比です。
今回の問題に当てはめると、以下のようになります。
この式を変形して、求めたい高低差 $h$ を計算するためには、**サイン（sin）**を使用するのが正解となります。
3. コサイン（cos）とタンジェント（tan）はいつ使うか？
もし問題で水平距離を求める必要があった場合は、以下のように使い分けます。
| 三角関数 | 定義 | 測量での使用目的 |
| コサイン (cos) | （底辺）／（斜辺） | 水平距離を求める場合 （（水平距離） = D × cos α） |
| タンジェント (tan) | （対辺）／（底辺） | 水平距離と高低差が分かっている場合に角度を求める場合 |
この「求めたいものが直角三角形のどの辺か」という観点で考えると、三角関数の使い分けはスムーズになります。
↓ほかの問題も見たい方はこちら↓
令和2年測量士補試験 解答解説
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 | 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 | 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士補試験におすすめのテキストについて→過去の記事に飛びます。
コメント
答え 300.18ではないでしょうか？
D×sinαの部分を確認お願いします。
コメントいただきありがとうございます。
確認したところ、問題の模範解答は「300.18 m」でした。
300.177をまるめた値が300.18ですので、計算過程は修正せず、
どの選択肢が模範解答か追記しました。
サインコサインタンジェントの使い分けが分かりません。
なぜこの場合はサインなのでしょうか
コメントありがとうございます。
sinとcosの使い分けは「求めたいものが直角三角形のどの辺か」という観点で考えると、三角関数の使い分けはスムーズになります。
今回は直角三角形の「斜辺」の長さを求めたいのでsinを使用しました。