これは試験前に解き方を丸暗記がよいと思う。
でも理解していると確実に解ける問題です。
問題
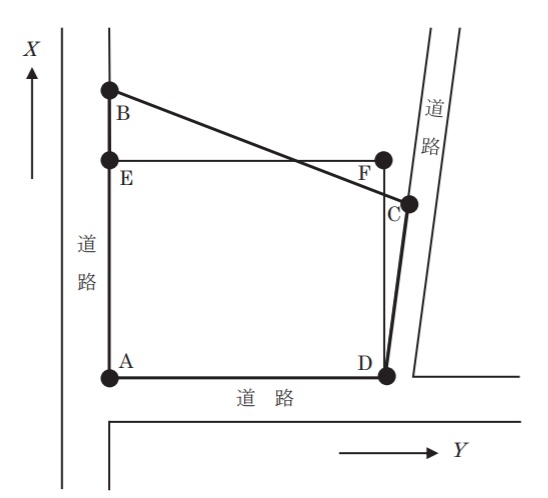
図27は、境界点A、B、C、Dの順に直線で結んだ土地を表したもので、土地を構成する各境界点の平面直角座標系（平成14年国土交通省告示第 9 号）に基づく座標値は表のとおりである。公共測量によって、土地ABCDの面積の90 ％となる長方形AEFDに整えたい。このとき境界点FのX 座標値は幾らか。最も近いものを次の中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
| 境界点 | X座標（ｍ） | Y座標（ｍ） |
| A | -20.630 | -17.800 |
| B | +79.370 | -17.800 |
| C | +39.370 | +86.200 |
| D | -20.630 | +78.200 |
１．+49.430 m
２．+53.870 m
３．+55.120 m
４．+58.630 m
５．+75.750 m
解答
正解は選択肢３です。
ステップ１ 四角形ABCDの面積を求める
四角形ABCDの面積は下表から8080m2。（表を作ると計算が楽）
下表を作るための計算手順を覚えよう
①Y座標に関して（Yn+1-Yn-1）を計算する。
②①にX座標値を掛け算する。（(Yn+1-Yn-1)×Xn）
③各境界点ごとの②をすべて足し合わせ、２で割る。四角形の面積が算出される。
| 境界点 | X座標（ｍ） | Y座標（ｍ） | Yn+1-Yn-1 | (Yn+1-Yn-1)×Xn |
| A | -20.630 | -17.800 | -17.800-78.2=-96.000 | (-96.000)×(-20.630)=1980.48 |
| B | +79.370 | -17.800 | 86.200-(-17.800)=104.000 | 104.000×79.370=8254.48 |
| C | +39.370 | +86.200 | 78.200-(-17.800)=96.000 | 96.000×39.370=3779.52 |
| D | -20.630 | +78.200 | -17.800-86.200=-104.00 | (-104.00)×(-20.630)=2145.52 |
| 合計÷2 | 16160.00÷2=8080.00 |
ステップ２ 四角形AEFDの面積を求める
問題文より
（四角形AEFDの面積）＝（四角形ABCDの面積）×0.9
=8080 × 0.9 =7272m2
ステップ３ 辺FDの長さを求める
FD=（四角形AEFDの面積）÷（辺ADの長さ）
＝7272÷（78.2-17.8）
＝7272÷96
＝75.75
ステップ4 点FのX座標を求める
（点FのX座標）＝75.750-20.630=55.12
↓ほかの問題も見たい方はこちら↓
令和2年測量士補試験 解答解説
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 | 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 | 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士補試験におすすめのテキストについて→過去の記事に飛びます。
コメント