試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第25問 問題
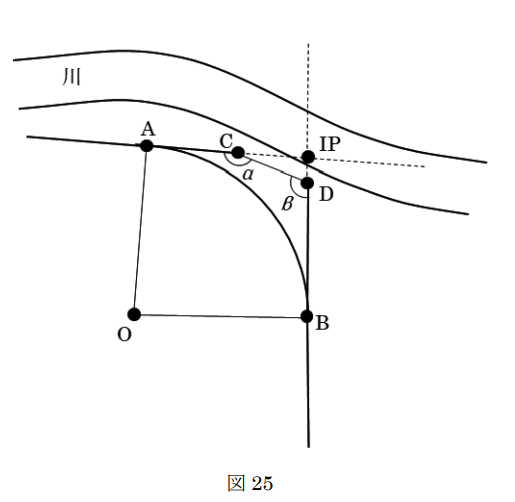
図25は、平たんな土地における、円曲線始点A、円曲線終点Bからなる円曲線の道路建設の計画を模式的に示したものである。交点IPの位置に川が流れており、杭を設置できないため、点Aと交点IPを結ぶ接戦上に補助点C、点Bを交点IPを結ぶ接戦上に補助点Dをそれぞれ設置し観測を行ったところ、α=170°、β=110°であった。曲線半径R=300mとするとき、円曲線始点Aから円曲線終点Bまでの路線長は幾らか。最も近いものを次の中から選べ。
なお、円周率π=3.14とし、関数の値が必要な場合は、巻末の関数表を使用すること。
選択肢
1.382 m
2.419 m
3.471 m
4.524 m
5.576 m
第25問 解答・解説
正解は選択肢2です。以下、解説。

図を描きながら解いていきましょう。
ステップ1 問題文で与えられている条件を図に記入
問題文で与えられた条件
曲線半径 R = 300 m,交角 α = 170°, 新道路の交角 β = 110°。
その他、問題を解くための前提知識
・円の接線は、その接点を通る半径に垂直
→∠CAO, ∠DBO=90°
・五角形の内角の和は540°
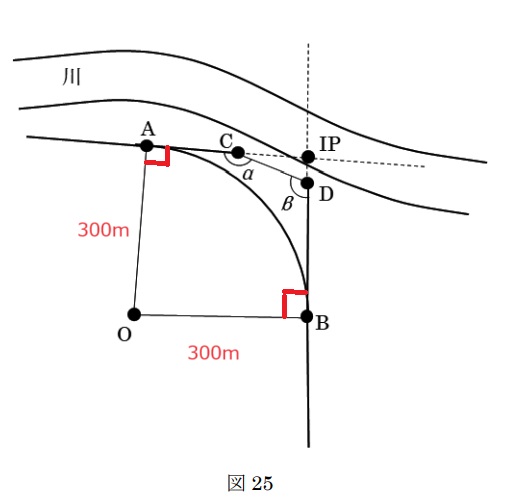
以下、五角形ACDBOに着目して計算していきます。
別解として三角形C IP Bに着目しても、∠AOBを算出可能です(360°-(α+β))。
ステップ2 図をもとに計算する
まずは∠AOBを求めます。
五角形の内角の和は540°、∠CAO, ∠DBO=90°、α = 170°, β = 110°であることから
∠AOB+∠CAO+∠DBO+α+β = 540°
∠AOB = 540° -(∠CAO+∠DBO+α+β)
= 540° – (90°+90°+170°+110°)
= 540° – 460°
= 80°
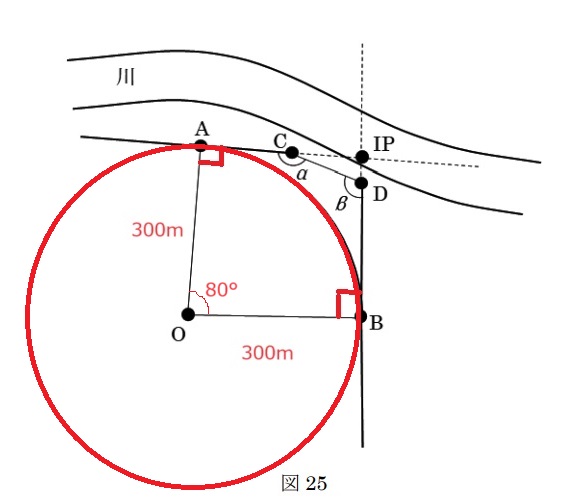
上図の赤線で示す円の円周は
2πr=2×3.14×300(m)=1884 m
よって、本問で求めるべき円曲線始点Aから円曲線終点Bまでの路線長は
1884 × 80°/360° = 418.66… m
= 419 m
以上、正解は選択肢2です。

類題を解きたい方は
測量士補試験令和4年第25問
を解いてみましょう。
どうしても計算問題が苦手な方へ おすすめしたい東京法経学院の有料講座
⇒わかる 測量士補試験の数学 これだけ! 公式15
↓ほかの問題も見たい方はこちら↓
| 法規 | 第1問 | 第2問 | 第3問 | 第4問 | |
| 基準点測量 | 第5問 | 第6問 | 第7問 | 第8問 | 第9問 |
| 水準測量 | 第10問 | 第11問 | 第12問 | 第13問 | |
| 地形測量 | 第14問 | 第15問 | 第16問 | ||
| 写真測量 | 第17問 | 第18問 | 第19問 | 第20問 | |
| 地図 | 第21問 | 第22問 | 第23問 | 第24問 | |
| 応用測量 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士補試験の過去問解説→記事一覧に飛びます。
測量士補試験におすすめのテキストについて→過去の記事に飛びます。

コメント