試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第27問 問題
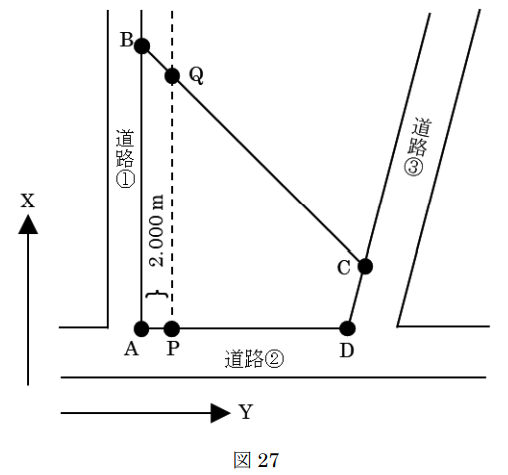
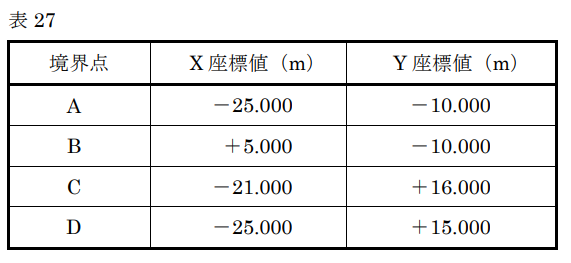
図27は、境界点A, B, C,Dで囲まれた四角形の土地を表したもので、境界点A及び境界点Bは道路➀との境界となっている。また、土地を構成する各境界点の平面直角座標系(平成14年国土交通省告示第9号)に基づく座標値は表27のとおりである。
道路➀が拡幅されることになり、新たな境界線PQが引かれることとなった。直線ABと直線PQが平行であり、拡幅の幅が2,000mである場合、点P, Q, C, Dで囲まれた四角形の土地の面積は幾らか。最も近いものを次の中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
選択肢
1.368 m2
2.382 m2
3.440 m2
4.476 m2
5.502 m2
第27問 解答・解説
正解は選択肢2です。以下、解説。

図を描きながら解いていきましょう。
ステップ1 四角形ABCDの面積を求める
四角形ABCDの面積は下表から440m2。(表を作ると計算が楽)

下表を作るための計算手順を覚えよう
①Y座標に関して(Yn+1 – Yn-1)を計算する。
②①にX座標値を掛け算する。((Yn+1 – Yn-1) × Xn)
③各境界点ごとの②をすべて足し合わせ、2で割る。四角形の面積が算出される。
| 境界点 | X座標(m) | Y座標(m) | Yn+1-Yn-1 | (Yn+1-Yn-1)×Xn |
| A | -25.000 | -10.000 | -10.000-15.000=-25.000 | (-25.000)×(-25.000)=625.000 |
| B | +5.000 | -10.000 | 16.000-(-10.000)=26.000 | 26.000×5.000=130 |
| C | -21.000 | +16.000 | 15.000-(-10.000)=25.000 | 25.000×(-21.000)=-525 |
| D | -25.000 | +15.000 | -10.000-16.000=-26.000 | (-26.000)×(-25.000)=650 |
| 合計(2S) | 880m2 | |||
| 合計÷2 | 880÷2=440m2 |
ステップ2 四角形PQCDの面積を求める
図より本問で求めるべき四角形PQCDは次の式で求められる
(四角形PQCDの面積)=(四角形ABCDの面積)-(四角形ABQPの面積)
そこでまずは、四角形ABQPの面積を求める。
台形の面積を求める公式((上底+下底)× 高さ ÷ 2)より
(四角形ABQPの面積)=((辺AB)+(辺PQ))×(辺AP)÷ 2
=(30+28)×2 ÷ 2 =58m2
※上式での辺の長さの求め方
表よりA(-25, -10), B(5, -10), P(-25, -8), Q(3, -8)
辺AB = |5 – (-25)| = 30
辺PQ = |3 – (-25)| = 28
辺AP = |-8 – (-10)| = 2
よって、図より本問で求めるべき四角形PQCDは
(四角形PQCDの面積)=(四角形ABCDの面積)-(四角形ABQPの面積)
= 440 – 58 = 382m2
以上、正解は選択肢2です。
↓ほかの問題も見たい方はこちら↓
測量士補試験の過去問解説→記事一覧に飛びます。
測量士補試験におすすめのテキストについて→過去の記事に飛びます。


コメント