試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第27問 問題
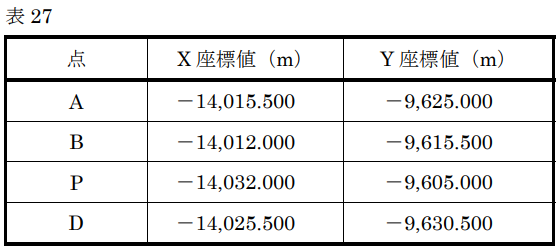
境界点A、B、C、Dで囲まれた四角形の土地の面積を求めたい。点Cは直接観測できないため、補助基準点Pを設置し、点A、B、P、Dをトータルステーションを用いて測量し、表27に示す平面直角座標系(平成14年国土交通省告示第9号)における座標値を得た。点A、B、C、Dで囲まれた四角形の土地の面積は幾らか。最も近いものを次の中から選べ。
ただし、補助基準点Pから点Cまでの距離は10.000 m、点Pにおける点Cの方向角は330°とする。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
選択肢
1.114.202 m2
2.160.050 m2
3.227.550 m2
4.285.035 m2
5.354.707 m2
第27問 解答・解説
正解は選択肢2です。
以下、解説。

筆者はこの分野が苦手なので計算過程のみ解説します。
図示する
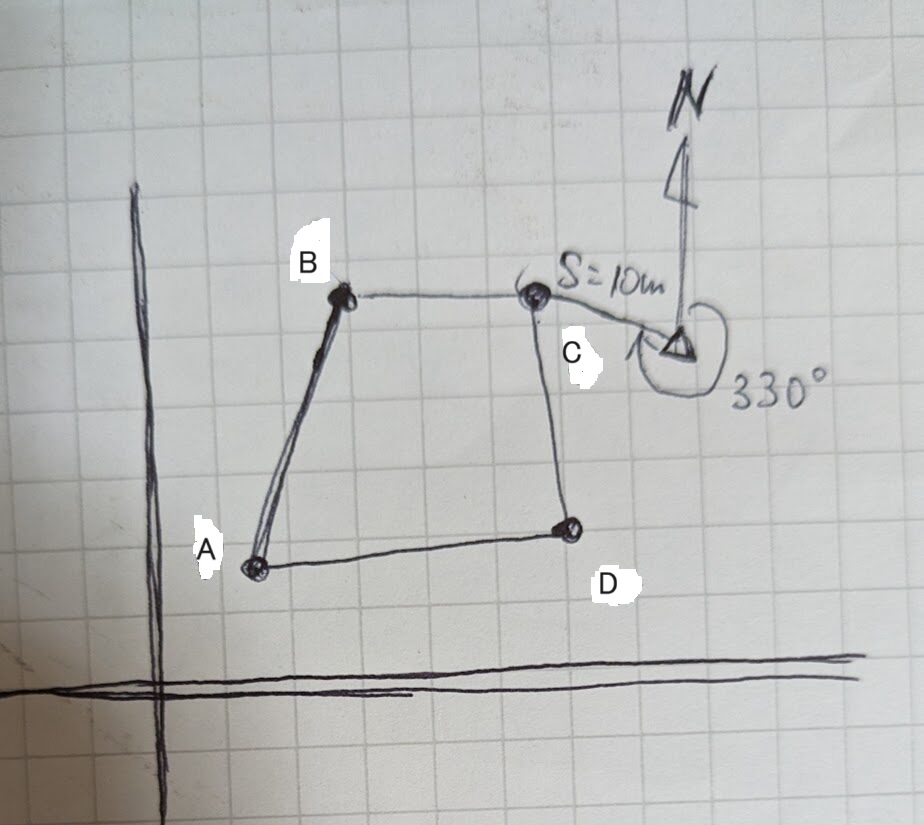
計算していく
| 点 | 方向角(α) | 距離(S) | X m | Y m |
| P | -14,032.000 | -9,605.000 | ||
| 330° | 10 m | ΔX=8.6603 | ΔY=-5.000 | |
| B | -14,023.340 | -9,610.000 |
次に、座標原点をX=-14,000、Y=-9,600移動して各点の座標値を計算の容易な数値に変換する。
| 点 | Xi m | Yi m |
| A | -14,015.500 | -9,625.000 |
| B | -14,012.000 | -9,615.500 |
| C | -14,023.340 | -9,610.000 |
| D | -14,025.500 | -9,630.500 |
| 点 | Xi m | Yi m |
| A | 15.500 | 25.000 |
| B | 12.000 | 15.500 |
| C | 23.340 | 10.000 |
| D | 25.500 | 30.500 |
変換後の座標により座標面積計算を行い四角形ABCDの面積を求めると次表のとおり。
| 境界点 | X座標(m) | Y座標(m) | Yn+1-Yn-1 | (Yn+1-Yn-1)×Xn |
| A | 15.500 | 25.000 | 15.500-30.500=-15.000 | (-15.000)×15.500=-232.5 |
| B | 12.000 | 15.500 | 10.000-25.000=-15.000 | (-15.000)×12.000=-180.00 |
| C | 23.340 | 10.000 | 30.500-15.500=15.000 | 15.000×23.340=350.1 |
| D | 25.500 | 30.500 | 25.000-10.000=15.000 | 15.000×25.500=382.5 |
| 合計(2S) | 320.1m2 | |||
| 合計÷2 | 320.1÷2=160.05m2 |
よって最も近い面積は選択肢2の160.050 m2。
正解は「選択肢2」。

類題
令和5年測量士補試験 第27問
令和元年測量士(午前)第27問
↓ほかの問題も見たい方はこちら↓
測量士試験(午前)の過去問解説→記事一覧に飛びます。


コメント