試験問題の引用
令和3年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html

追記:過去問演習ができるページを開設しました。
フィードバックいただけると嬉しいです。
第3問 問題
次の文の「 ア」 及び「 イ」 に入る数値の組合せとして最も適当なものはどれか。次の中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
点 A、B、C、D で囲まれた四角形の平たんな土地 ABCD について、幾つかの辺長と角度を観測したところ、∠ABC=90 °、∠DAB = 105 °、AB = BC = 20 m、AD = 10 m であった。
このとき AC = 「ア」 m であり、土地 ABCD の面積は「 イ」 m2 である。
| ア | イ | |
| 1. | 28.284 | 270.711 |
| 2. | 28.284 | 322.475 |
| 3. | 34.641 | 150.000 |
| 4. | 34.641 | 286.603 |
| 5. | 34.641 | 350.000 |
第3問 解答・解説
正解は選択肢2です。
ステップ1 図を描く
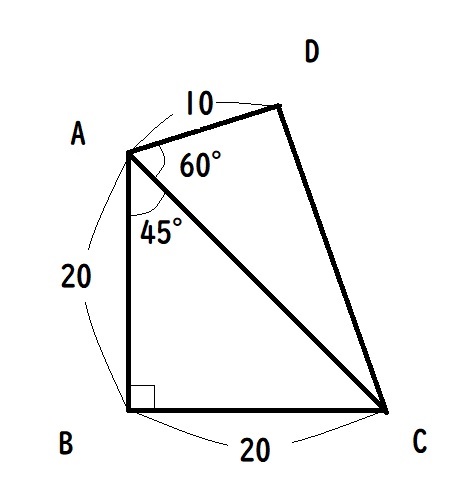

図示してみると、三角定規のあの形かなとイメージしたくなりますね。
でも、∠ADCは直角ではありません。
ステップ2 辺ACの長さを求める
三角形ABCについて、三平方の定理より
AC2=AB2+BC2
=202+202=800
AC=√800=20√2
=20×1.41421=28.2842
よって、空欄「ア」に当てはまるACの長さは28.284 m
ステップ3 四角形の面積を求める
三角形ABC+三角形ACDと考えて四角形の面積を算出します。
三角形ABC の面積
直角三角形なので簡単ですね。
( 三角形ABC の面積 )=AB×BC÷2=20×20÷2=200
三角形ACD の面積
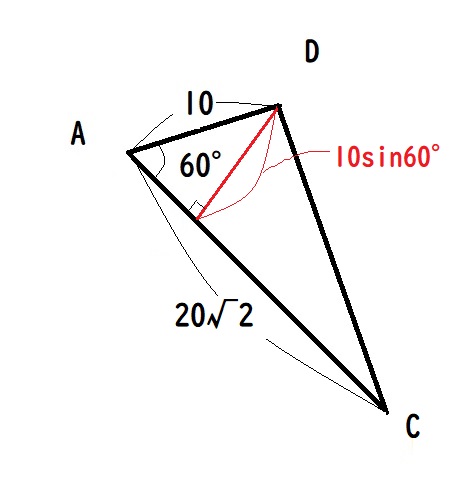
上図のように補助線を引いてあげると求めやすくなります。
( 三角形ACD の面積 )=AC× 10sin60° ÷2=20√2 × (10×√3÷2) ÷2=50√6=122.4745
よって、
(求める四角形の面積)=122.4745+200=322.4745 「イ」
ゆえに選択肢2が正解です。
令和3年測量士補試験 解答解説
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 | 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 | 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
令和2年測量士補試験の解説→令和2年測量士補試験第1問の解説記事に飛びます。
測量士補試験におすすめのテキストについて→過去の記事に飛びます。

コメント