試験問題の引用
令和4年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html

測量士補試験の過去問演習ができるページがありますので、
フィードバックいただけると改善の参考にします。
第27問 問題
地点 A,B,C で囲まれた三角形 ABC の土地の面積を算出するため,公共測量で設置された4 級基準点から,トータルステーションを使用して測量を実施した。 4 級基準点から三角形の頂
点にあたる地点 A,B,C を観測した結果は表 27 のとおりである。この土地の面積は幾らか。
最も近いものを次の中から選べ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
| 地点 | 方向角 | 平面距離 |
| A | 45°00’00” | 50.000 m |
| B | 90°00’00” | 20.000 m |
| C | 330°00’00” | 50.000 m |
1.945 m2
2.1006 m2
3.1067 m2
4.1128 m2
5.1189 m2
第27問 解答・解説
正解は選択肢4です。以下、解説。

図を描きながら解いていきましょう。
手順① 地点A,B,Cの座標を求める
表27の情報から地点A,B,Cの座標を求めます。
1.地点Aの座標
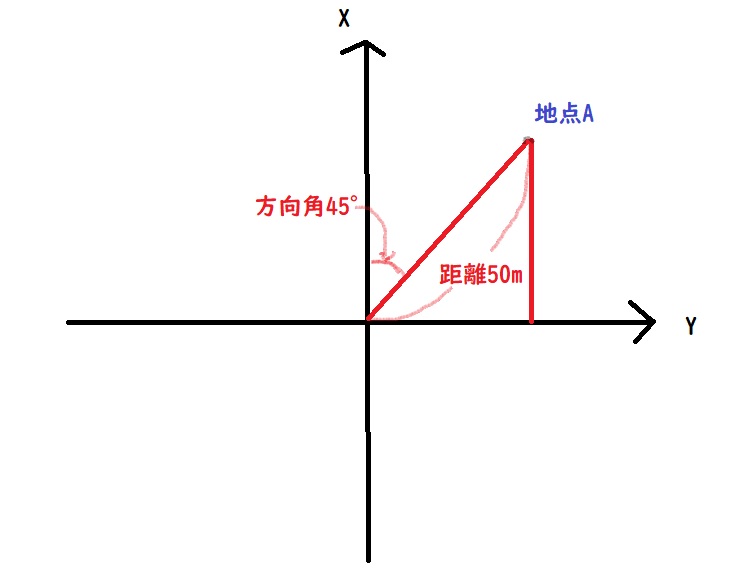
X座標:50 m × sin45°=50×0.70711=35.3555≒35.356
Y座標:50 m × cos45°=50×0.70711=35.3555≒35.356
2.地点Bの座標
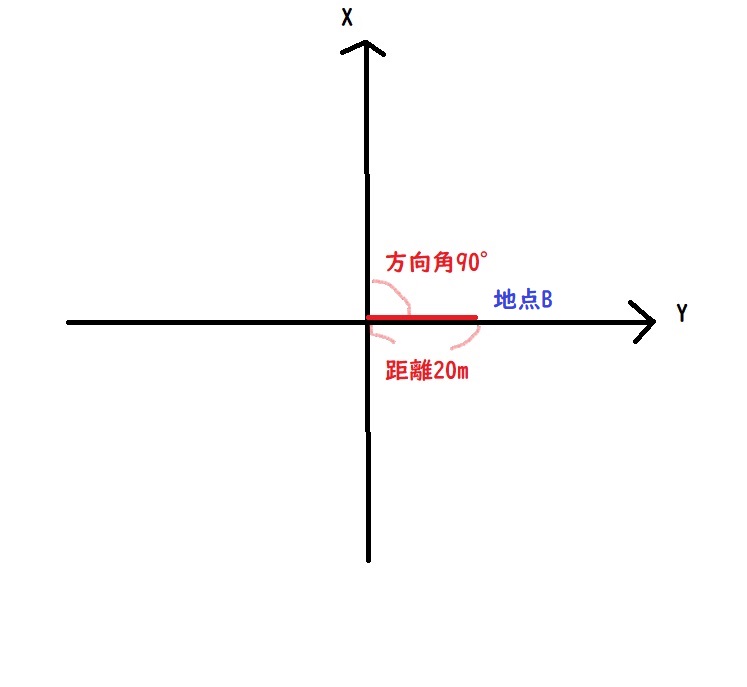
X座標:0
Y座標:20
3.地点Cの座標
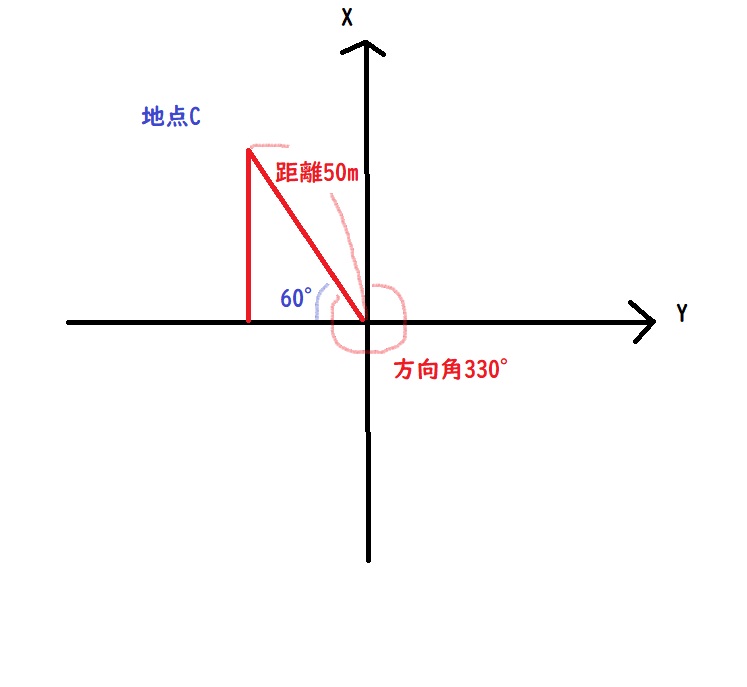
X座標:50 m × sin60°=50×0.86603=43.3015≒43.302
Y座標:50 m × cos60°=50×0.50000=25
→Y座標はマイナス側に位置しているため-25
手順② 座標法を用いて三角形ABCの面積を求める
手順①で算出した値を一覧表にすると下表のようになる。
| 測点 | X座標 | Y座標 |
| A | 35.356 | 35.356 |
| B | 0 | 20 |
| C | 43.302 | -25 |
三角形ABCの面積は次式で求められる。
①Y座標に関して(Yn+1-Yn-1)を計算する。
②①にX座標値を掛け算する。((Yn+1-Yn-1)×Xn)
③各境界点ごとの②をすべて足し合わせ、2で割る。三角形の面積が算出される。
| 測点 | Xn(m) | Yn(m) | Yn+1-Yn-1 | (Yn+1-Yn-1)×Xn |
| A | 35.356 | 35.356 | 20-(-25)=45 | 45×35.356=1591.02 |
| B | 0 | 20 | -25-35.356=-60.356 | (-60.356)×0=0 |
| C | 43.302 | -25 | 35.356-20=15.356 | 15.356×43.302=664.946 |
| 合計÷2 | (1599.12+0+664.946)÷2=1127.983 |
よって求める三角形ABCの面積は1128m2
以上、正解は選択肢4です。
↓ほかの問題も見たい方はこちら↓
測量士補試験の過去問解説→記事一覧に飛びます。
令和3年測量士補試験の解説→令和3年測量士補試験第1問の解説記事に飛びます。
令和2年測量士補試験の解説→令和2年測量士補試験第1問の解説記事に飛びます。
測量士補試験におすすめのテキストについて→過去の記事に飛びます。


コメント