試験問題の引用
令和6年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第３問 問題
次のa及びbの各問の答えとして最も近いものの組合せはどれか。次の1～5の中なら選べ。
ただし、円周率π=3.14とする。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
a. 84°15′ 36”をラジアンに換算すると幾らか。
b. 三角形ABCで辺AC=8.0 m, ∠BCA=70°, ∠ABC=30°としたとき、辺BCの長さは幾らか。
選択肢
| a | b | |
| 1. | 0.73ラジアン | 4.1 m |
| 2. | 0.73ラジアン | 15.8 m |
| 3. | 1.47ラジアン | 15.0 m |
| 4. | 1.47ラジアン | 15.8 m |
| 5 | 4.83ラジアン | 15.0 m |
第３問 解答・解説
正解は選択肢４です。
令和2年測量士補試験第3問でも類題が出題されています。
繰り返し解いて解き方を覚えましょう。
以下、解説。
a
a. 84°15′ 36”をラジアンに換算すると幾らか。
計算手順１ 度分秒から10進法に変換
84° → 84°
15’ → 15÷60 = 0.25
36” → 36÷60÷60 = 0.01
よって、
84°+0.25+0.01 = 84.26°
計算手順２ 10進法からラジアンに変換
求めたい値をAと置くと下記の通り。
180° : π = 84.26° : A
180° × A = 84.26° × π
A = 84.26°× π ÷ 180°
A = 1.47061…
≒ 1.47 ラジアン
b
b. 三角形ABCで辺AC=8.0 m, ∠BCA=70°, ∠ABC=30°としたとき、辺BCの長さは幾らか。
計算手順１ ∠BACを求める
∠BAC = 180° – ∠BCA – ∠ABC
= 180° – 70° – 30°
= 80°
計算手順２ 辺BCの長さを求める
与えられた条件と上記手順１にて得られた結果を図示すると次の通り
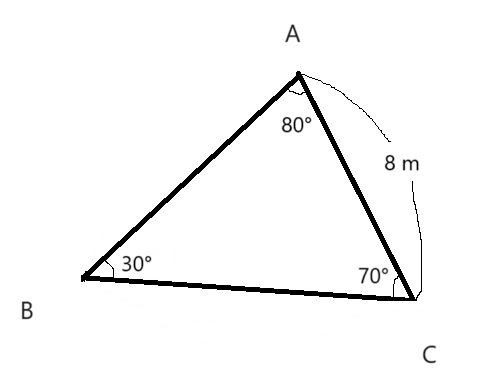
正弦定理より
BC / sin80° = AC / sin30°
BC = AC / sin30° × sin80°
BC = 8 ÷ 0.5 × 0.98481
BC = 15.75696
≒ 15.8 m
以上、正解は「選択肢４」でした。
令和6年測量士補試験の解説は随時更新予定です。
↓ほかの問題も見たい方はこちら↓
測量士補試験の過去問解説→記事一覧に飛びます。
測量士補試験におすすめのテキストについて→過去の記事に飛びます。
コメント