試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第13問 問題
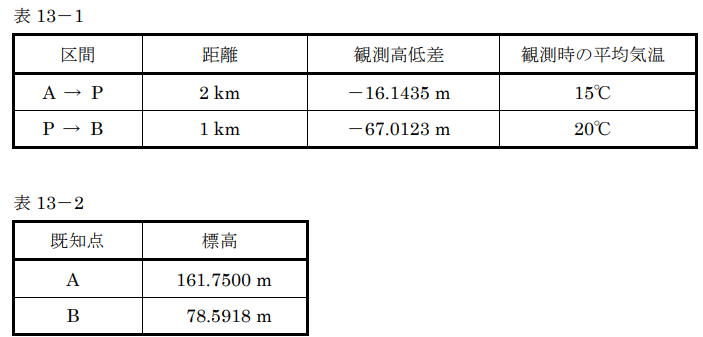
既知点A及び既知点Bから新点Pの標高を求めるため、公共測量における1級水準測量を行い、表13-1の結果を得た。標尺補正を行った後の新点Pの標高の最確値は幾らか。最も近いものを次の中から選べ。
ただし、既知点A及び既知点Bの標高は表13-2のとおりであり、この観測で使用した標尺の標尺改正数は20℃において+5μm/m、膨張係数は+1.0×10-6/℃である。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
選択肢
1.145.6047 m
2.145.6051 m
3.145.6053 m
4.145.6055 m
5.145.6058 m
第13問 解答・解説
正解は選択肢2です。
以下、解説。
ステップ1 標尺補正計算をする
標尺補正をする式は次のように定義される
ΔC=(C0+(T-T0)×α)×Δh
ΔC:標尺補正量
C0:標尺改正数(1mあたり)
T:観測した温度
T0:基準温度
α:膨張係数(1mあたり)
Δh:観測高低差
上記公式に問題文の値を代入すると標尺補正量が求められる。
区間A→Pの標尺補正量
ΔCA=(C0+(T-T0)×α)×Δh
= (( +5.0 × 10-6 + ( 15 – 20 ) × 1.0× 10-6 )× (-16.1435 m)
= (( 5.0 × 10-6 + ( – 5 × 10-6 ) )× (-16.1435 m) )
= 0 × (-16.1435 m)
= 0
点Pの標尺補正後の観測高低差
161.7500 m – 16.1435 m + 0 m
= 145.6065 m
区間P→Bの標尺補正量
ΔCB=(C0+(T-T0)×α)×Δh
= ( +5.0 × 10-6 + ( 20 – 20 ) × 1.0× 10-6 ) × (-67.0123 m)
= ( 5.0 × 10-6 + ( 0 ) × 10-6 ) × (-67.0123 m)
= -335.0615 × 10-6m
= -0.0003350615 m
≒ -0.0003 m
点Pの標尺補正後の観測高低差(点PからBに向かう観測なので符号を-にしています)
78.5918 m – (- 67.0123 m + (-0.0003 m) )
=78.5918 m – ( -67.0126 m)
= 145.6044 m
ステップ2 最確値を求める(重量平均計算)
観測距離から重量比を求める。
1/2 : 1/1 =1 : 2
標高の最確値を求める。重量比とステップ1で求めた標尺補正後の観測値より
((1×145.6065 m) + 2×(145.6044 m)) / (1+2)
=(145.6065 m + 291.2088 m) / 3
=436.8153 m / 3
=145.6051 m
正解は「選択肢2」。

上記問題は、過去の測量士補試験の問題を合わせた問題となっています。
標尺補正の計算問題:令和2年測量士補第13問
標高の最確値を求める問題:令和3年測量士補第13問
どうしても計算問題が苦手な方へ おすすめしたいアガルートの有料講座(税込27,280円)
⇒測量士試験|パターンで攻略!計算問題
↓令和5年測量士試験(午前) 解答解説↓
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 |
| 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 |
| 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士試験(午前)の過去問解説→記事一覧に飛びます

コメント