試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第3問 問題
次の文のア 及び イ に入る数値の組合せとして最も適当なものはどれか。次の中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
三角形ABCで∠ABCの角度を同じ条件で5回測定し、表3の結果を得た。このとき、∠ABCの角度の最確値の標準偏差の値はア となる。
また、表3の測定値の最確値を∠ABCの角度とし、辺ABの辺長を3.0m、辺BCの辺長を8.0mとしたとき、辺CAの辺長は イ となる。
| 測定値 |
| 59°59’57” |
| 60° 0′ 1” |
| 59°59’59” |
| 60° 0′ 5” |
| 59°59’58” |
選択肢
| ア | イ | |
| 1. | 1.4” | 7.0 m |
| 2. | 1.4” | 9.8 m |
| 3. | 2.8” | 5.6 m |
| 4. | 2.8” | 9.8 m |
| 5. | 3.2” | 7.0 m |
第3問 解答・解説
正解は選択肢1です。以下、解説。
空欄ア
ア.1.4”
イ.7.0 m
最確値とは
最も確からしいと考えられる値であり、一般的に最小二乗法で求めた値である。
今回の問題では同一条件での観測であるため、最小二乗法ではなく算術平均で十分である。
計算手順① 最確値を求める
| 測定値 |
| 59°59’57” |
| 60° 0′ 1” |
| 59°59’59” |
| 60° 0′ 5” |
| 59°59’58” |
問題文で与えられている表3より次の式で算出可能。
(59°59’57”+60°0’1”+59°59’59”+60°0’5”+59°59’58”)÷5
=297°177’180” ÷ 5
=59.4°35.4’36”
=59.4°35’24”+36”
=59°24’+35’+1’0”
=60°0’0”
小数点は60をかけて処理しています。(度分秒なので)
(最確値の別の求め方)
表3の観測値がすべて60°前後であることに着目し60°0’00’と観測値との差から最確値を求める。
(-3” + 1” – 1” +5” -2” )÷ 5 = 0”
よって、最確値は60° 0′ 0′

今回は測定条件が同一だったため、最確値=平均値です。
(重量平均が必要な場合は算出方法が異なります)
計算手順② 計算しやすいように表を作る
| 観測回数 | 測定値 | δ | δ2 |
| 1 | 59°59’57” | -3” | 9 |
| 2 | 60° 0′ 1” | 1” | 1 |
| 3 | 59°59’59” | -1” | 1 |
| 4 | 60° 0′ 5” | 5” | 25 |
| 5 | 59°59’58” | -2” | 4 |
| 平均 60° 0′ 0” | 合計 40 |
計算手順③ 標準偏差を求める
√(Σ δ2÷n(n-1))
=√(40÷5(5-1))
=√(40÷(5×4))
=√2
=1.4
よって、最確値の標準偏差は1.4”である。
空欄イ
イ.7.0 m
辺CAの長さを求めるために問題文の情報を図示してみる。
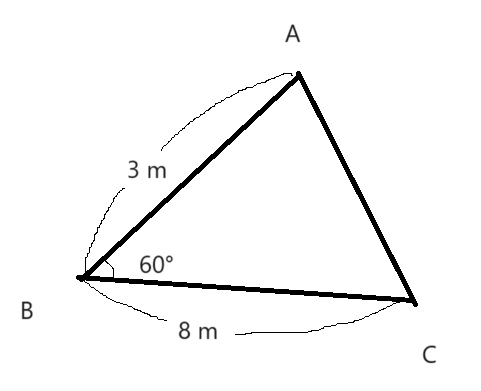
三角形の2辺とその間の角度がわかっているため余弦定理より
CA2 = 32 + 82 -2 × 3 × 8 × cos60°
= 9 +64 – (48 × 1/2 )
= 73 – 24
= 49
CA = 7 m
以上、正解は選択肢2です。
類題

令和2年測量士補試験 第6問、令和3年測量士補試験 第3問で測量の誤差に関する出題がありました。
復習にご活用ください。
どうしても計算問題が苦手な方へ おすすめしたい東京法経学院の有料講座
⇒わかる 測量士補試験の数学 これだけ! 公式15
↓ほかの問題も見たい方はこちら↓
| 法規 | 第1問 | 第2問 | 第3問 | 第4問 | |
| 基準点測量 | 第5問 | 第6問 | 第7問 | 第8問 | 第9問 |
| 水準測量 | 第10問 | 第11問 | 第12問 | 第13問 | |
| 地形測量 | 第14問 | 第15問 | 第16問 | ||
| 写真測量 | 第17問 | 第18問 | 第19問 | 第20問 | |
| 地図 | 第21問 | 第22問 | 第23問 | 第24問 | |
| 応用測量 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士補試験の過去問解説→記事一覧に飛びます。

コメント