令和5年測量士試験（午前）　第８問（計算：距離の観測）を解説

第８問　問題

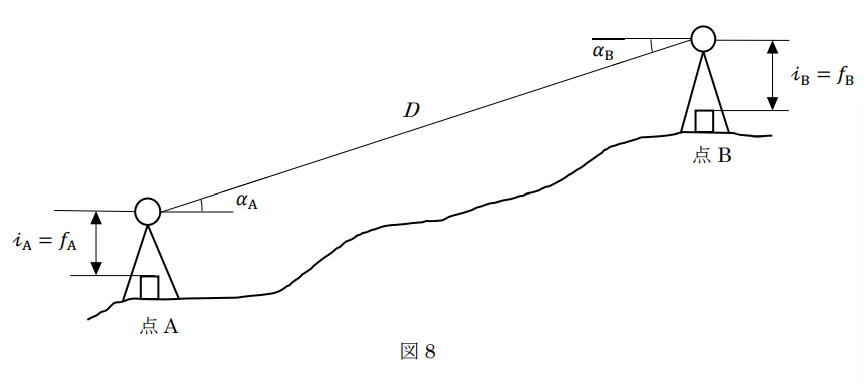
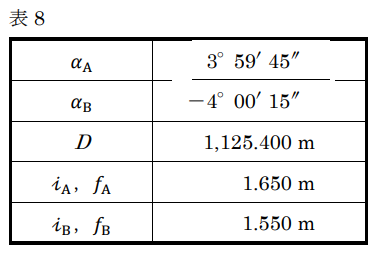
　公共測量におけるトータルステーションを用いた1級基準点測量において、図8に示すように、標高16.10mの点Aと標高94.70mの点Bとの間の距離及び高低角の観測を行い、表8の観測結果を得た。Dを斜距離、α_Aを点Aから点B方向の高低角、α_Bを点Bから点A方向の高低角、i_A、f_A、を点Aの器械高及び目標高i_B、f_Bを点Bの器械高及び目標高とするとき、点A、点B間の基準面上の距離はいくらか。最も近いものを次の中から選べ。
　ただし、地球の平均曲率半径は6,370km、点A、点Bのジオイド高を平均した値は43.00mを用いるものとする。また、Dは気象補正等必要な補正がすでに行われているものとする。
　なお、関数の値が必要な場合は、巻末の関数表を使用すること。

選択肢
１．1,122.58 m
２．1,122.60 m
３．1,122.62 m
４．1,122.64 m
５．1,122.66 m

第８問　解答・解説

正解は選択肢４です。
以下、解説。

公式を覚えていれば解けます

令和元年測量士試験にも類題が出題されていますので、余力のある人は覚えましょう。

計算していく

上で示したx,y,z軸それぞれを軸に回転させた場合の座標変換式のうち、本問問われているy軸まわりの計算をする。

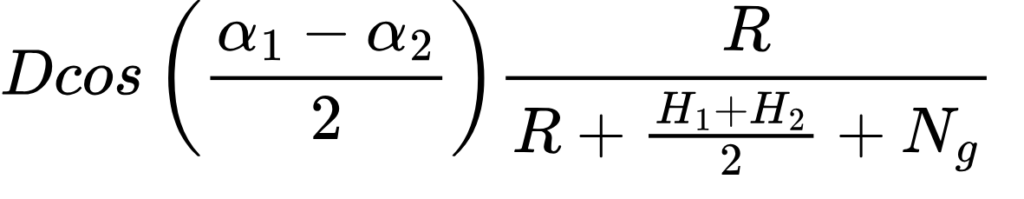
((α_A-α_B)/2) = ((3°59’45”-(-4°00’15”))/2)
= 8°00’00”/2 = 4°00’00”
cos4°＝0.99756

((H₁-H₂)/2) = ((16.10 + 1.650) + (94.70 + 1.550) / 2)
= 114 / 2 = 57 m

S = 1125.400 × 0.99756 × 6370000 / (6370000+57+43.00)
= 1125.400 × 0.99756 × 6370000 / 6370100
= 1122.6364
≒ 1122.64 m

正解は「選択肢４」。

↓ほかの問題も見たい方はこちら↓
測量士試験（午前）の過去問解説→記事一覧に飛びます。