試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第5問 問題
次の文は、測量の誤差について述べたものである。ア~ウに入る数式又は数値の組合せとして最も適当なものはどれか。次のページの中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
測量の誤差には、測定の条件が変わらなければ大きさや現れ方が一定した系統誤差と、誤差の原因が不明又は原因が分かってもその影響が除去できない偶然誤差がある。
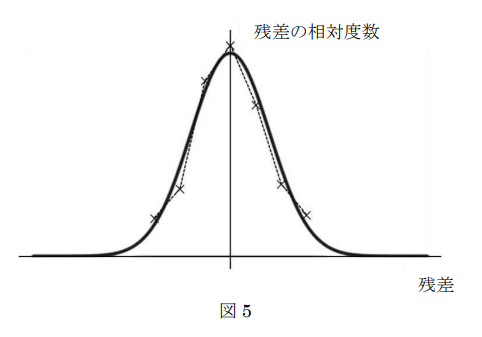
偶然誤差だけを含む一群の測定値について、残差の値を横軸に、残差の相対度数を縦軸にとってプロットした点を結ぶと、例として図5の破線のようなグラフが得られる。もし、測定回数を限りなく増やしたとすると、破線の形状は実践のように左右対称の曲線になると考えられ、偶然誤差の分布は、一般に正規分布に従うと仮定される。
正規分布の確率密度関数は、平均値をμ、標準偏差をσとすると、 ア で表される。 ア 式中の((x-μ)/σ)を式5のようにZとおくと、 ア はZについての平均値0、標準偏差1の標準正規分布として取り扱うことができ、正規分布表を使うことができる。

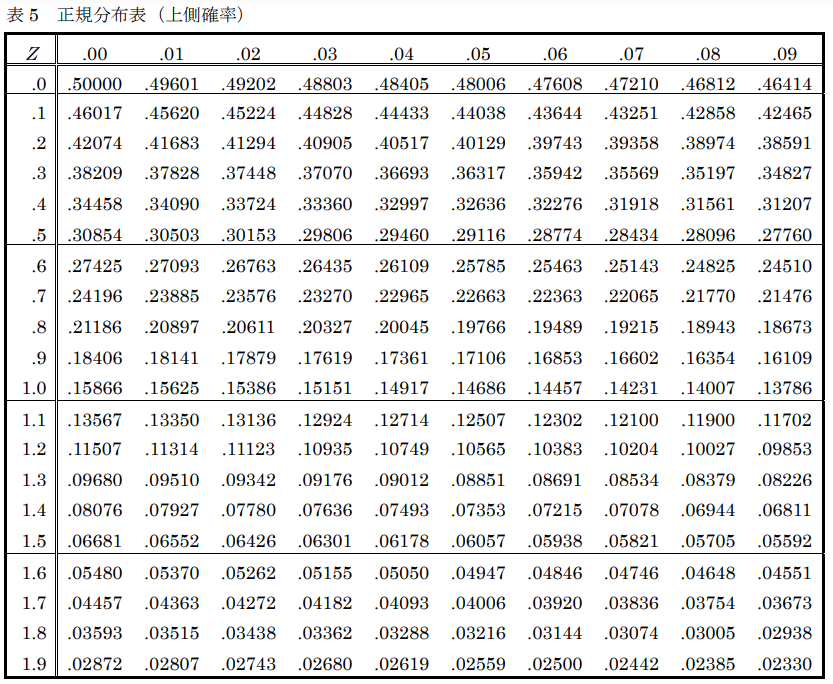
例えば、ある距離の偶然誤差だけを含む一群の測定値について、平均値が100.000m、標準偏差が0.012mの結果を得たとする。このとき、観測距離が100.020m以上となる確率を求める場合、式5のZの値として イ を用いることで、表5に示す正規分布表(上側確率)を使って ウ %を得る。
選択肢

第5問 解答・解説
正解は選択肢3です。
以下、解説。
今回解説記事を作成するにあたり参考にしたサイト「いちばんやさしい、医療統計」。

苦手な人は空欄イだけでも解けるように!
本文を読めば標準偏差を知らなくても空欄イは解けますよ!
空欄ア
正規分布の確率密度関数は、平均値をμ、標準偏差をσとすると、 ア で表される。 ア 式中の((x-μ)/σ)を式5のようにZとおくと、 ア はZについての平均値0、標準偏差1の標準正規分布として取り扱うことができ、正規分布表を使うことができる。
アに当てはまるのは下式です。
これは確率密度関数の定義なのでしっかり暗記しましょう。
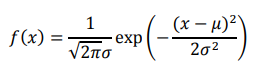
空欄イ、ウ
例えば、ある距離の偶然誤差だけを含む一群の測定値について、平均値が100.000m、標準偏差が0.012mの結果を得たとする。このとき、観測距離が100.020m以上となる確率を求める場合、式5のZの値として イ を用いることで、表5に示す正規分布表(上側確率)を使って ウ %を得る。
イ 問題文中の式5に文中で示された数字を入れるだけで解けます。
観測距離x=100.020m、平均値μ=100.000m、標準偏差σ=0.012m

Z =((x-μ)/σ)= ((100.020 – 100.000)/0.012)
= 0.020 / 0.012 = 1.666 ≒ 1.67
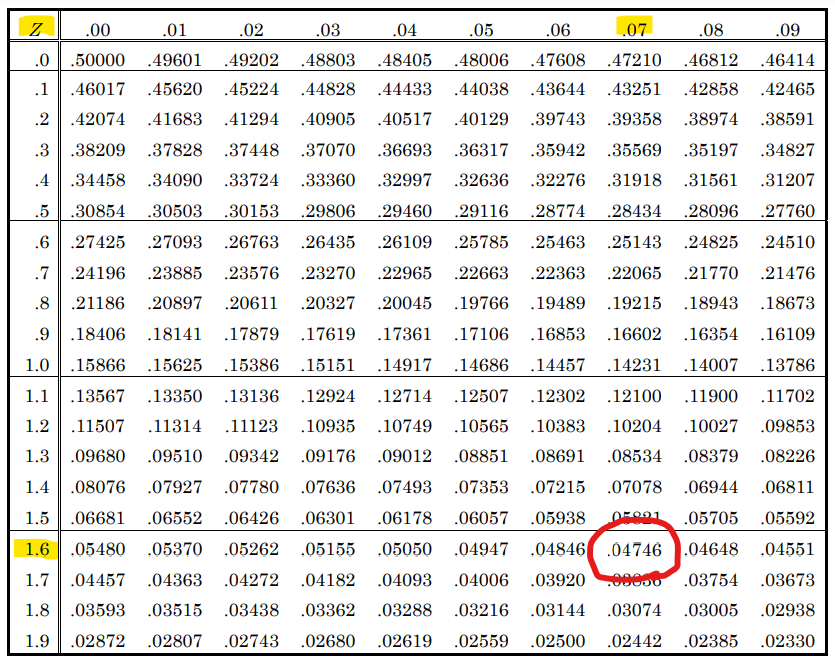
ウ イの値が表5のどこかわかれば解けます。
Zの値が1.67なので、縦軸「1.6」,横軸「0.07」の値が答えとなります。
よって答えは0.04746=4.746%
以上、正解は「選択肢3」でした。
↓ほかの問題も見たい方はこちら↓
測量士試験(午前)の過去問解説→記事一覧に飛びます。


コメント