試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第25問 問題
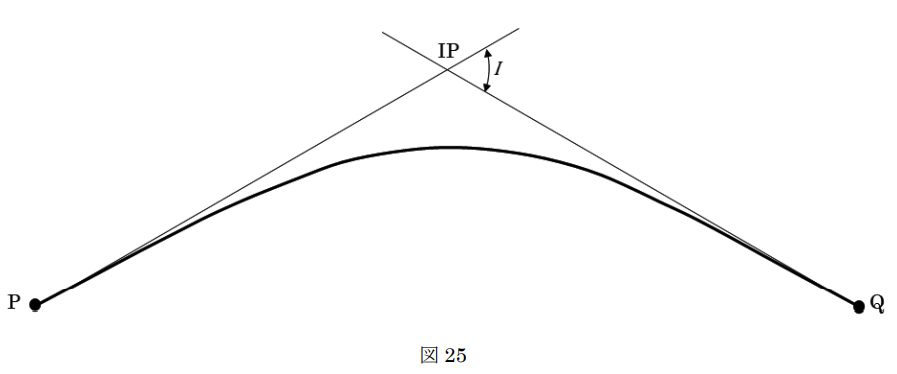
図25に示すように、点Pを始点、点Qを終点とする基本型クロソイド(対称型)の道路の建設を計画している。円曲線部の半径R=180 m、交角I=60°、クロソイドパラメータA=110 m、円周率π=3.142とするとき、点Pから点Qまでの路線長は幾らか。最も近いものを次の中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
選択肢
1.256 m
2.312 m
3.361 m
4.428 m
5.483 m
第25問 解答・解説
正解は選択肢1です。
以下、解説。

筆者はこの分野が苦手なので計算過程のみ解説します。
図示する
計算していく
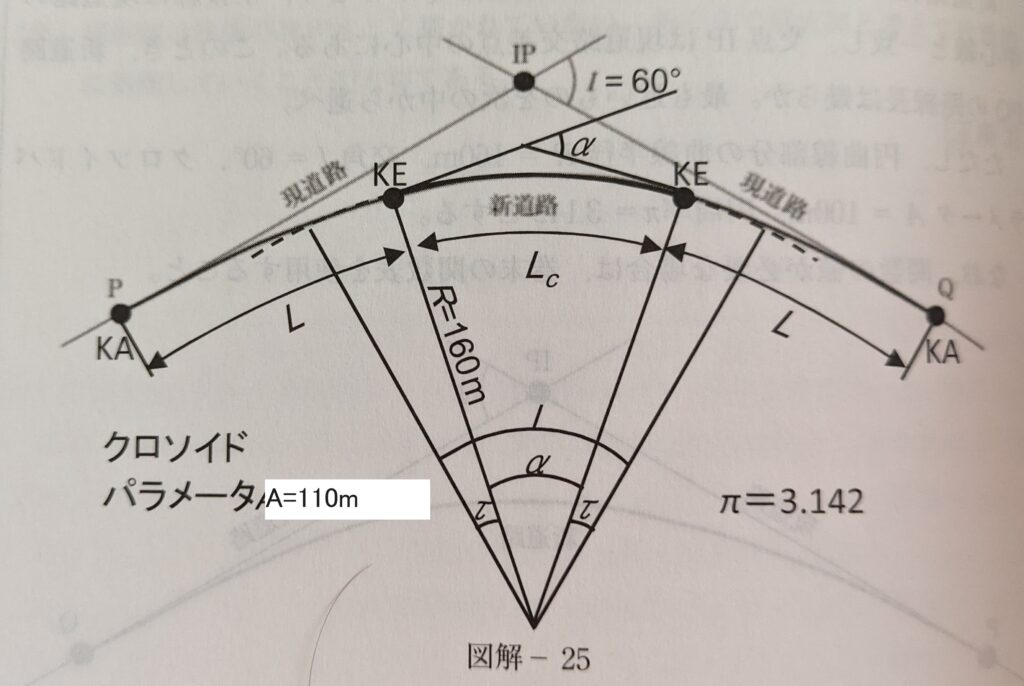
新路線PQの路線長は図解-25で示す通り
(クロソイド長(L))× 2 +(円曲線長(Lc))
Lはクロソイドの基本公式で
L=A2/Rより
L=1102 / 180 = 67.2 m
Lcについては図解-25より α=I-2τ になり、
τについては τ=L/(2R) という公式(※)より
α=I-2(L/(2R)) = I-L/R
Lc=Rαであるので、Lc=R(I-L/R)=RI-L
したがって新路線長は
L+Lc+L=L+(RI-L)+L=RI+L
=180×60×π/180 + 67.2
=188.52 + 67.2
=255.72 m
よって求める新路線長は255.72 m。
正解は「選択肢1」。

類題
平成28年測量士試験(午前)第25問
(※)補足:τ=L/(2R) という公式
τ=L/(2R) は、測量士試験の「路線測量(曲線測量)」の分野で使われる、接線角(接線偏角)を求めるための公式です。
公式 τ=L/(2R) の意味
| 記号 | 意味 | 単位 |
| τ(タウ) | 接線角(接線偏角) | ラジアン (rad) |
| L | 曲線長(始点から任意の点までの長さ) | メートル (m) |
| R | 曲線半径 | メートル (m) |
何を計算するために使うのか?
この公式は、路線(道路や鉄道の設計線)を実際に地上に設置する(測設する)際に使用します。
円曲線の始点(BC点)から、曲線上の任意の点(設置したい点)を観測機械(トータルステーションなど)を使って正確に測るために必要な水平角(接線角)を計算します。
- 接線角の定義: 曲線始点(BC点)の接線(直線)を基準(0度)としたとき、曲線上の任意の点に向かう方向線が接線となす角度のことです。
どうしても計算問題が苦手な方へ おすすめしたいアガルートの有料講座(税込27,280円)
⇒測量士試験|パターンで攻略!計算問題
↓令和5年測量士試験(午前) 解答解説↓
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 |
| 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 |
| 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士試験(午前)の過去問解説→記事一覧に飛びます

コメント
τ=L/(2R)って何の公式ですか?
ご質問ありがとうございます。
ご質問の公式 τ=L/(2R) は、測量士試験の「路線測量(曲線測量)」の分野で使われる、接線角(接線偏角)を求めるための公式です。
これは円曲線の計算において、非常に基礎的かつ重要な公式の一つです。