試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第14問 問題
図14のように、高低差Zを求めるために、トータルステーション(以下「TS」という。)を用いて、放射法により既知点Aから求点Bを観測した。
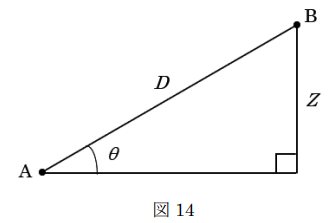
既知点Aから求点Bまでの斜距離をD、高低角をθ、高低差をZとすると、高低差Zは式14-1で表される。
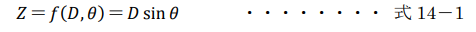
斜距離D、高低角θそれぞれの観測値の標準偏差をσD、σθとする。
また、TSによる距離測定と角度測定はお互いに影響を与えないものとし、その他の誤差は考えないものとする。
斜距離Dと高低角θの観測がお互いに独立であることから、両者の共分散は0となる。それぞれの観測値の分散をσD2、σθ2とした場合、高低差ZのσZ2分散は、誤差伝播の法則から式14-2で求められる。
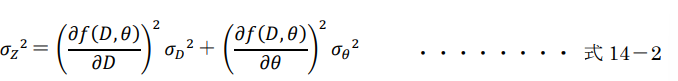
ここで、既知点Aから求点Bを観測した測定値は、斜距離の測定距離D0= 200.000 m、高低角θ0= 30°00’00”であり、使用したTSの距離測定の精度(標準偏差)は(5+5×10-6D)mm(Dはmm単位の測定距離)、角度測定の精度(標準偏差)は5”とする。このとき、高低差Zの標準偏差σZは幾らか。最も適当なものを次のページの中から選べ。
ただし、式14-1及び14-2の距離の単位はmm、角度の単位はラジアンとし、1ラジアンは(2×105)”とする。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
選択肢
1.3.91 mm
2.4.13 mm
3.5.27 mm
4.6.19 mm
5.6.76 mm
第14問 解答・解説
正解は選択肢3です。
以下、解説。
(ブログ筆者は標準偏差が苦手なので計算過程のみ記します)
ステップ1 D = D0,θ = θ0 のときの値を計算する
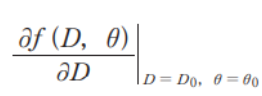
アを求めるためにf(D,θ)をDで微分する。
f'(D,θ) = sinθ
θ=θ0を代入。高低差θ0は問題文より30°
sin30°=0.5
斜距離Dの標準偏差σDを求める。
問題文より「使用した TS の距離測定の精度(標準偏差)は(5 + 5 × 10-6D)mm(D は mm 単位の測定距離)」、「斜距離の測定距離 D0 = 200.000 m」
σD = 5 + 5×10-6×200000=5+1.0 =6.0
f(D,θ)をθで微分する。
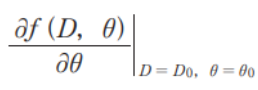
f'(D,θ) = Dcosθ
θ=θ0=30°、D=D0=200.000 mのときDcosθは
D0cosθ0 = 200000 × cos30°=200000×0.86603=173206
標準偏差σθを求める。
題文中の「角度 1 ラジアンは,(2 × 105)” 」、「角度測定の精度(標準偏差)を 5″」、「D = D0,θ = θ0 のときの具体的な数値は,距離の単位を mm,角度の単位をラジアンとすると次のように計算できる」から空欄エは次の式で求まる。

問題文中で角度測定の標準偏差は5”とあるので、それをラジアンに変換するだけです。
5” ÷ (2×105) = 0.000025
ステップ2 上記をもとに高低差Zの標準偏差σZを求める
上記で求めた答えを下記の式14-2に代入する。
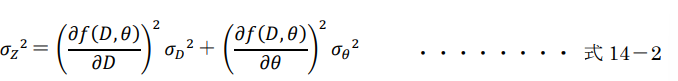
0.52 × 6.02 +1732062 × 0.0000252
=0.25 × 36 + 18.7502
=27.7502
≒ 27.75
√27.75 = 5.27 mm
正解は「選択肢3」。
↓ほかの問題も見たい方はこちら↓
測量士試験(午前)の過去問解説→記事一覧に飛びます。


コメント