試験問題の引用
令和4年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第27問 問題
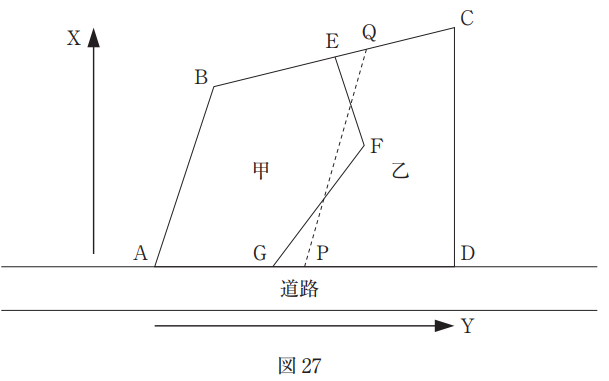
図 27 は,境界点 E,F,G を順に直線で結んだ境界線で区切られた甲及び乙の土地を表したものであり,土地を構成する各境界点の平面直角座標系(平成 14 年国土交通省告示第 9 号)における座標値は表 27 のとおりである。甲及び乙のそれぞれの土地の面積を変えずに,境界点 P,Qを設置して直線 PQ で区切られた土地に新たに区割りする場合,点 Q の X 座標の値は幾らか。最も近いものを次のページの中から選べ。
ただし,境界点 P は,甲及び乙の土地の道路に接している長さが等しくなる位置(AP = PD)とする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
| 境界点 | X(m) | Y(m) |
| A | +13060.00 | +11970.00 |
| B | +13090.00 | +11980.00 |
| C | +13100.00 | +12020.00 |
| D | +13060.00 | +12020.00 |
| E | +13095.00 | +12000.00 |
| F | +13080.00 | +12005.00 |
| G | +13060.00 | +11990.00 |
選択肢
1.+13,094.82 m
2.+13,095.25 m
3.+13,095.68 m
4.+13,096.11 m
5.+13,096.54 m
第27問 解答・解説
正解は選択肢4です。
以下、解説。

ねじれ図形の問題です。
過去、平成28年問27に出題されています。
手順1 図に情報を書き込む
今後の計算をしやすくするため点Aを原点(0,0)とする。
図27に表27と問題文の情報を書き込むと下図のようになる。
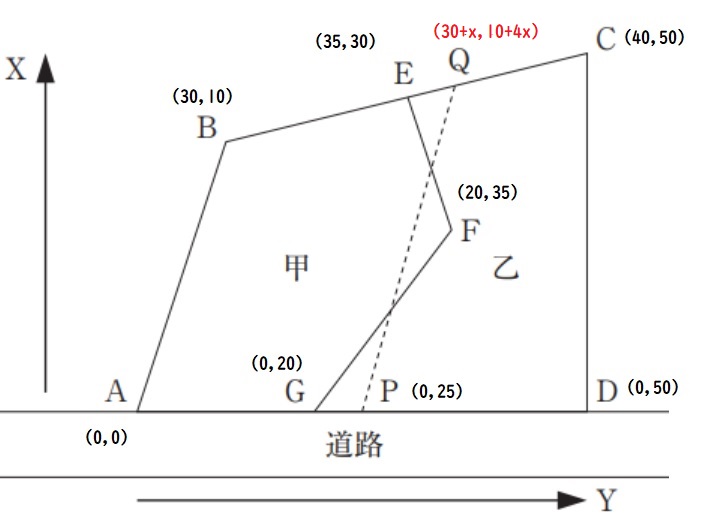
①点Pの座標(X座標値, Y座標値) を求める
表27より点A(0,0), 点D(0,50)という情報と
問題文の「AP = PD」という情報から点P(0,25)となる。
②点Qの座標(X座標値, Y座標値) を求める
私は点Qの座標を(30+x, 10+4x)としました。その考え方を下記に記します。
ちょっと特殊な考え方をしますので、図示します。
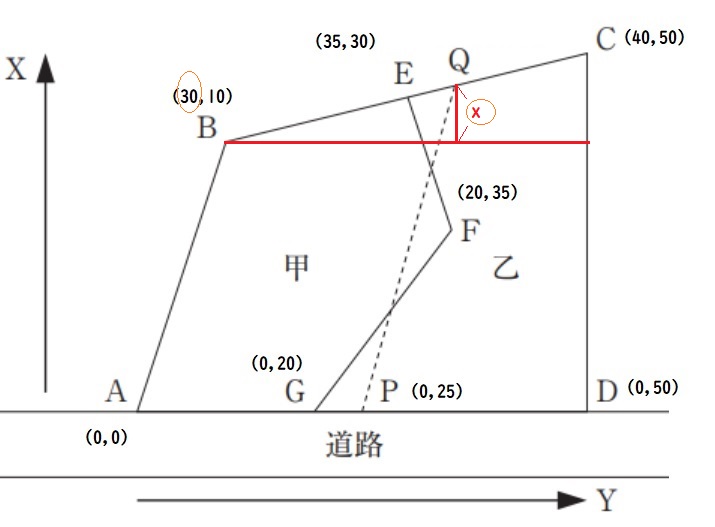
点Qの座標をなんとか一次関数で表したいので次の手順で座標を設定します。
1)点Qが直線BC上にあることに着目
2)点Bと点Q間のX軸方向の長さの差をxと置く。
3)点QのX座標値は「30+x」となる
ここからは点QのY座標値を求めるための考え方を書きます。
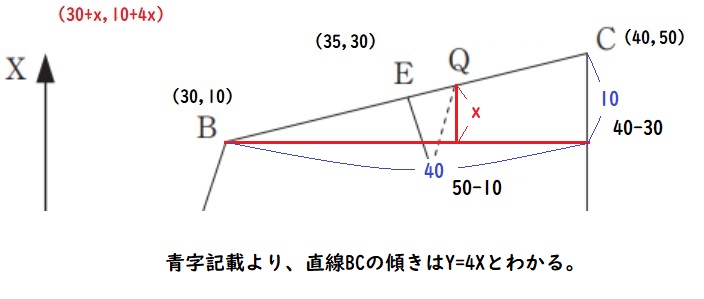
4)上図より点Bと点QのY軸方向の長さは「4x」となる。
4xの求め方。三角形の相似関係を利用して次のように考えられる。
40:10=y:x
40x=10y
10y=40x
y=4x
5)点QのY座標値は「10+4x」←点BのY座標値である10をプラスした。
ゆえに、点Bを起点に考えると点Qは(30+x,10+4x)と表せる。
手順2 ねじれ図形の面積を計算していく
ねじれ図形EFGPQの面積を計算する。
| 点 | X | Y | Yi+1 – Yi-1 | Xi (Yi+1 – Yi-1) |
| E | 35 | 30 | 25-4x | 35(25-4x) |
| F | 20 | 35 | -10 | -200 |
| G | 0 | 20 | -10 | 0 |
| P | 0 | 25 | 4x-10 | 0 |
| Q | 30+x | 10+4x | 5 | 5(30+x) |
| 合計 | 0 | 825-135x |
計算結果から
(825-135x) = 0
x ≒ 6.11
よって求める点Qの座標は
(30+x,10+4x) = (36.11,34.44)
さらに手順1で原点としていた点Aの座標値(13060,1970)を足すと
(13060+36.11,1970+34.44)≒(13096.11,2004.44)
ゆえに点 Q の X 座標の値は13096.11
以上、正解は「選択肢4」でした。

令和4年測量士試験の解説は随時更新予定です。
↓ほかの問題も見たい方はこちら↓
測量士試験(午前)の過去問解説→記事一覧に飛びます。


コメント
いつも大変勉強になっております。
手順一のQのy座標値は点B→点Cの傾きが4xとわかる。
よって点QのY座標は、10+4x
の立式の仕方を細かく教えていただけると助かります。
ほのか様
コメントいただきありがとうございます。
ご指摘の箇所について、記事を見直しました。
誤記の修正と図の追加をしましたのでご活用ください。
わかりやすく、尚かつ迅速な解説ありがとうございます。
いつもこちらのサイトには大変お世話になっております。