試験問題の引用
令和5年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html

測量士補試験の過去問演習ができるページがありますので、
フィードバックいただけると改善の参考にします。
第12問 問題
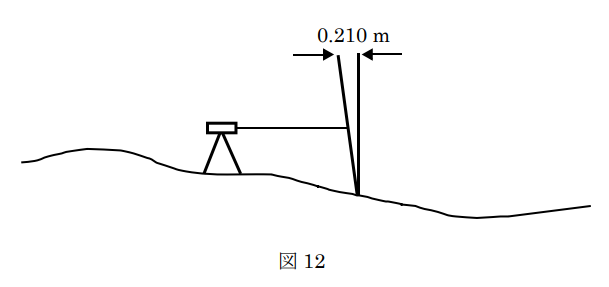
図12は、水準測量における観測の状況を示したものである。標尺の長さは3mであり、図12のように標尺がレベル側に傾いた状態で測定した結果、読定値が1.500mであった。標尺の上端が鉛直に立てた場合と比較してレベル側に水平方向で0.210mずれていたとすると、標尺の傾きによる誤差は幾らか。最も近いものを次の中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
選択肢
1. 4 mm
2.10 mm
3.14 mm
4.20 mm
5.24 mm
第12問 解答・解説
正解は選択肢1です。以下、解説。
➀標尺が何度傾いているか求める
三角関数を知っていると簡単に解ける問題です。
問題文からわかっていることを図示する。
標尺の長さは3m,標尺上端のズレは0.210m。
何度標尺が傾いてるかを算出するため角度をθと置きます。
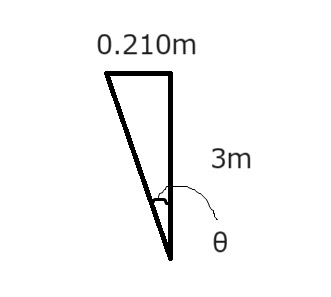
tanθ = 0.210 / 3 = 0.07
関数表よりθ=4°とわかる。
➁標尺の本来の読み値を求める
求めたい本来の標尺の読み値をaと置く。
標尺の読み値が1.5mであることから下記図の通りとなる。
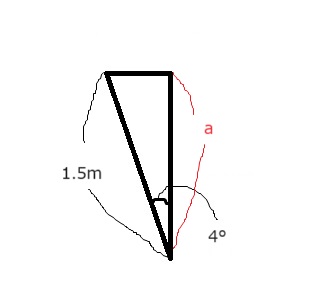
求めるaの長さは
1.5 × cos4° = 1.5 × 0.99756 = 1.49634
③標尺の傾きによる誤差を求める
計測時の読み値が1.5m,本来の読み値が1.49634であることから、求める誤差は
1.5 – 1.49634 = 0.00366 m = 3.66 mm
よって選択肢のうち、値が近い選択肢1の4mmが答えです。
以上、正解は選択肢1です。
どうしても計算問題が苦手な方へ おすすめしたい東京法経学院の有料講座
⇒わかる 測量士補試験の数学 これだけ! 公式15
↓ほかの問題も見たい方はこちら↓
| 法規 | 第1問 | 第2問 | 第3問 | 第4問 | |
| 基準点測量 | 第5問 | 第6問 | 第7問 | 第8問 | 第9問 |
| 水準測量 | 第10問 | 第11問 | 第12問 | 第13問 | |
| 地形測量 | 第14問 | 第15問 | 第16問 | ||
| 写真測量 | 第17問 | 第18問 | 第19問 | 第20問 | |
| 地図 | 第21問 | 第22問 | 第23問 | 第24問 | |
| 応用測量 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士補試験の過去問解説→記事一覧に飛びます。
測量士補試験におすすめのテキストについて→過去の記事に飛びます。

コメント
コメント失礼致します。
①の角度を求める式でtanθ=0.21/3=0.007となっておりますが、正しくは0.007ではなく0.07ではないでしょうか?
ごまふあざらし様
コメントいただきありがとうございます。
ご指摘箇所ですが、記載ミスでしたので修正させていただきました。