試験問題の引用
令和4年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第4問 問題
図 4 に示すような三次元直交座標系において,ある点(x,y,z)を z 軸のまわりに図 4 に示す方向に εz だけ回転させたときの点(x’,y’,z’)は次の式 4 で表される。
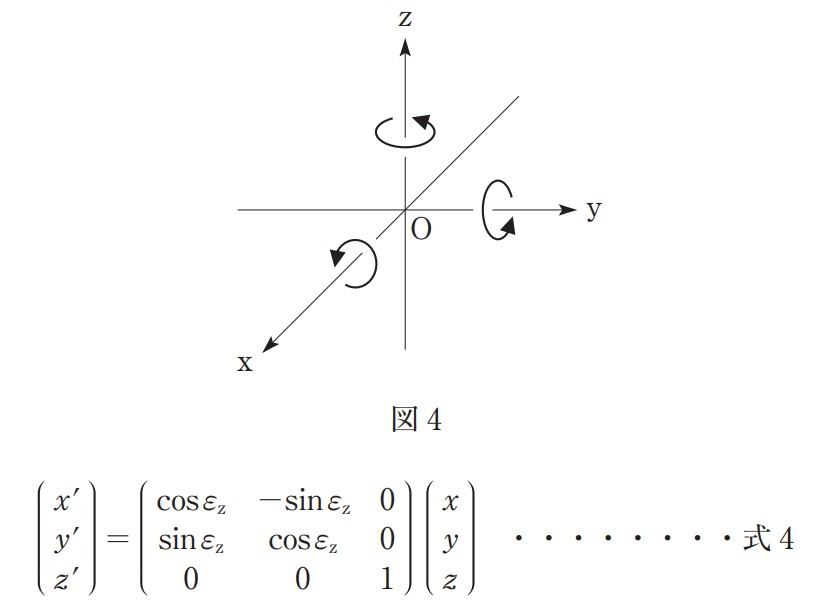
式 4 を参考に,点(x,y,z)を x 軸のまわりに図 4 に示す方向に εx だけ回転させる行列 Rxと,y 軸のまわりに図 4 に示す方向に εy だけ回転させる行列 Ry の組合せとして最も適当なものはどれか。次の中から選べ。
ただし,それぞれの回転後の点を(x”,y”,z”),(x’’’,y’’’,z’’’)とするとき,
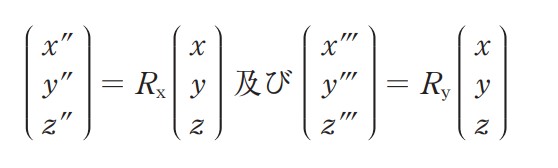
が成り立つ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
選択肢
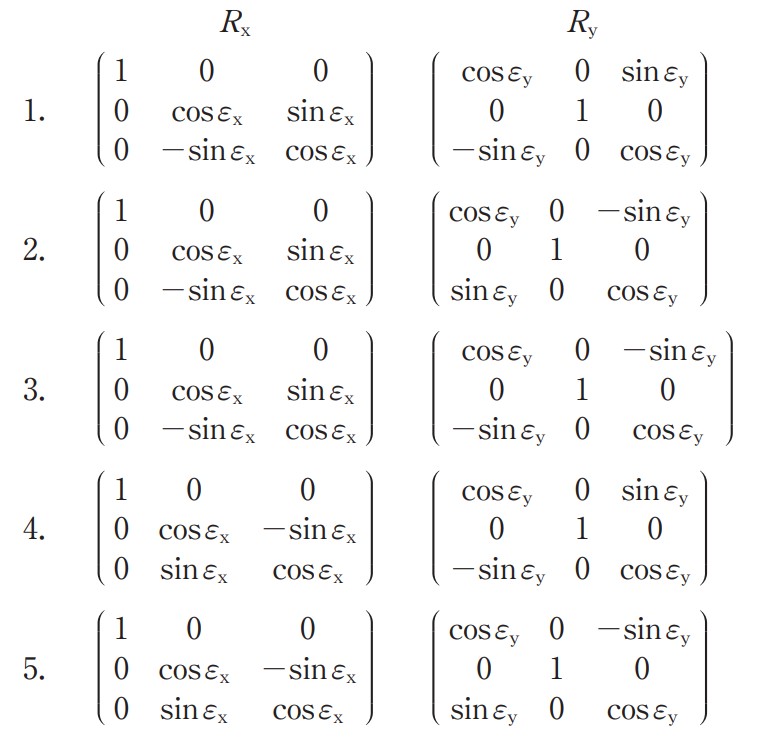
第4問 解答・解説
正解は選択肢4です。

補足:「ε」イプシロンと読みます。
以下、解説。
覚えていれば解けます
令和2年測量士試験にも類題が出題されていますので、x,y,z軸それぞれを軸に回転させた場合の座標変換式を覚えましょう。(いちいち式を導きだすのは大変ですから)


マイナス符号がどこにつくか覚えましょう
式を覚えない場合の考え方

フレミングの法則みたいに、自分の手を駆使してx,y,z軸の相対関係が崩れないように考えていきましょう。
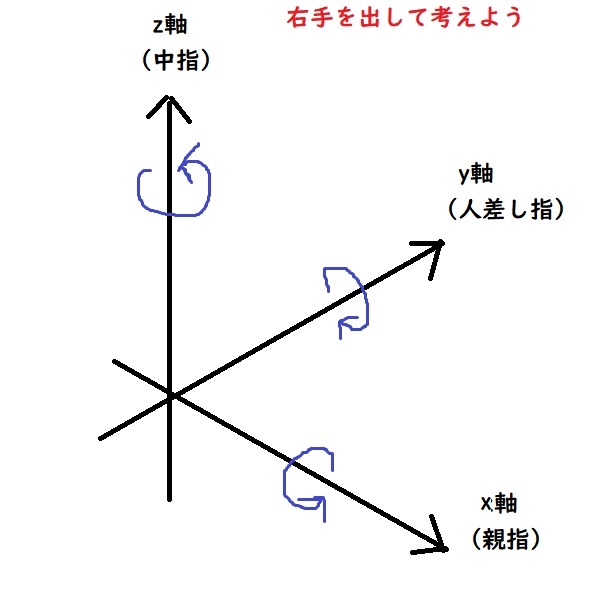
詳しくは別サイトにて解説がありましたので、そちらをご参照ください。
以上、正解は「選択肢4」でした。
どうしても計算問題が苦手な方へ おすすめしたいアガルートの有料講座(税込27,280円)
⇒測量士試験|パターンで攻略!計算問題
↓令和4年測量士試験(午前) 解答解説↓
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 |
| 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 |
| 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士試験(午前)の過去問解説→記事一覧に飛びます。

コメント