試験問題の引用
令和4年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第2問 問題
次の文は,地心直交座標系(平成 14 年国土交通省告示第 185 号)について述べたものである。
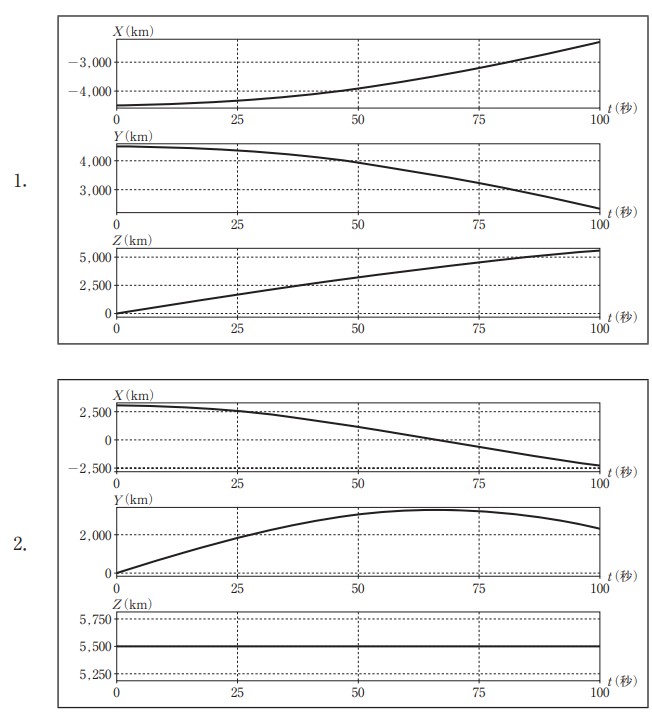
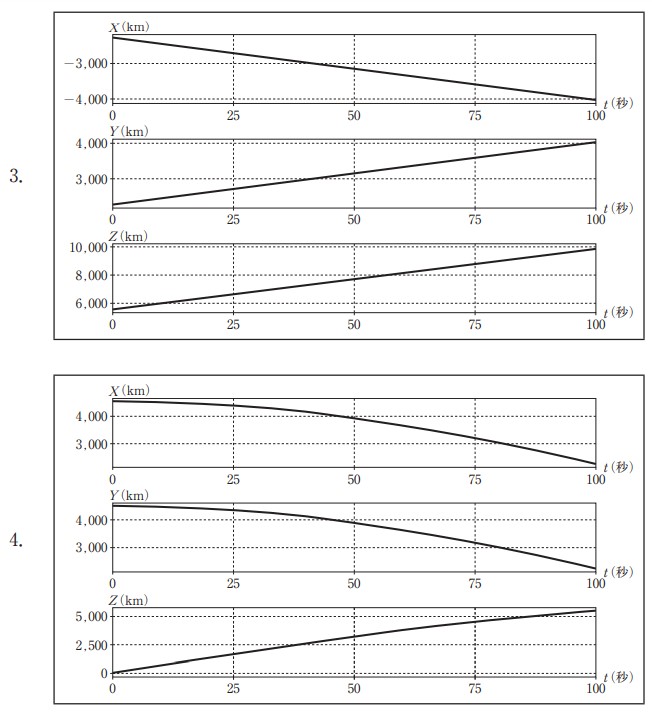
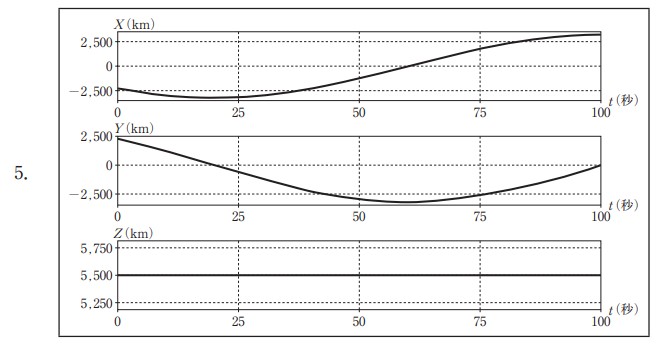
回転楕円体の表面上の点 A 及び点 B と,点 A,点 B を結ぶ表面上の最短経路を移動する点 Pを考える。点 A,点 B の位置は表 2 のとおりであり,点 P が時刻 t = 0 から t = 100(単位:秒)までの間に一定の速さで点 A から点 B へ移動するとき,時刻 t と点 P の地心直交座標系における座標値(X,Y,Z)との関係を表すグラフとして最も適当なものはどれか。次の中から選べ。
ただし,各グラフの横軸は時刻 t,縦軸は座標値(単位:km)を示している。
| 点名 | 緯度 | 経度 | 楕円体高 |
| A | 北緯 0°0’0” | 東経 135°0’0” | 0 m |
| B | 北緯 60°0’0” | 東経 135°0’0” | 0 m |
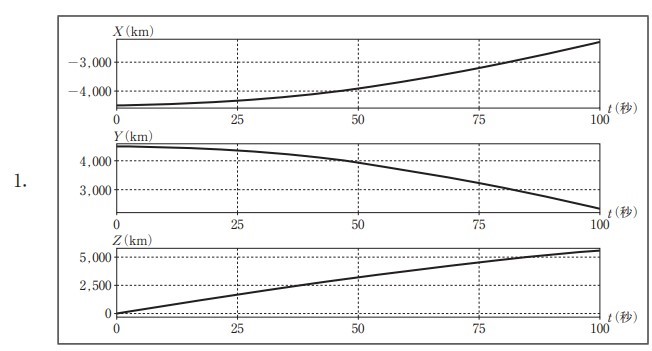
選択肢
第2問 解答・解説
正解は選択肢1です。

見たことのない出題形式で少し戸惑いますが、1つ1つ解き明かしていきましょう。
以下、解説。
地心直交座標とは?
問題をとくために、基礎をおさらいしましょう。
地心直交座標系は、法第十一条第三項に規定する扁平な回転楕円体の中心で互いに直交するX軸、Y軸及びZ軸の三軸からなり、各軸の要件は、次のとおりとする。
X軸は、回転楕円体の中心及び経度0度の子午線と赤道との交点を通る直線とし、回転楕円体の中心から経度0度の子午線と赤道との交点に向かう値を正とする。
Y軸は、回転楕円体の中心及び東経九十度の子午線と赤道との交点を通る直線とし、回転楕円体の中心から東経九十度の子午線と赤道との交点に向かう値を正とする。
Z軸は、回転楕円体の短軸と一致し、回転楕円体の中心から北に向う値を正とする。
地心直交座標系
少しわかりやすく書くと下のとおり。
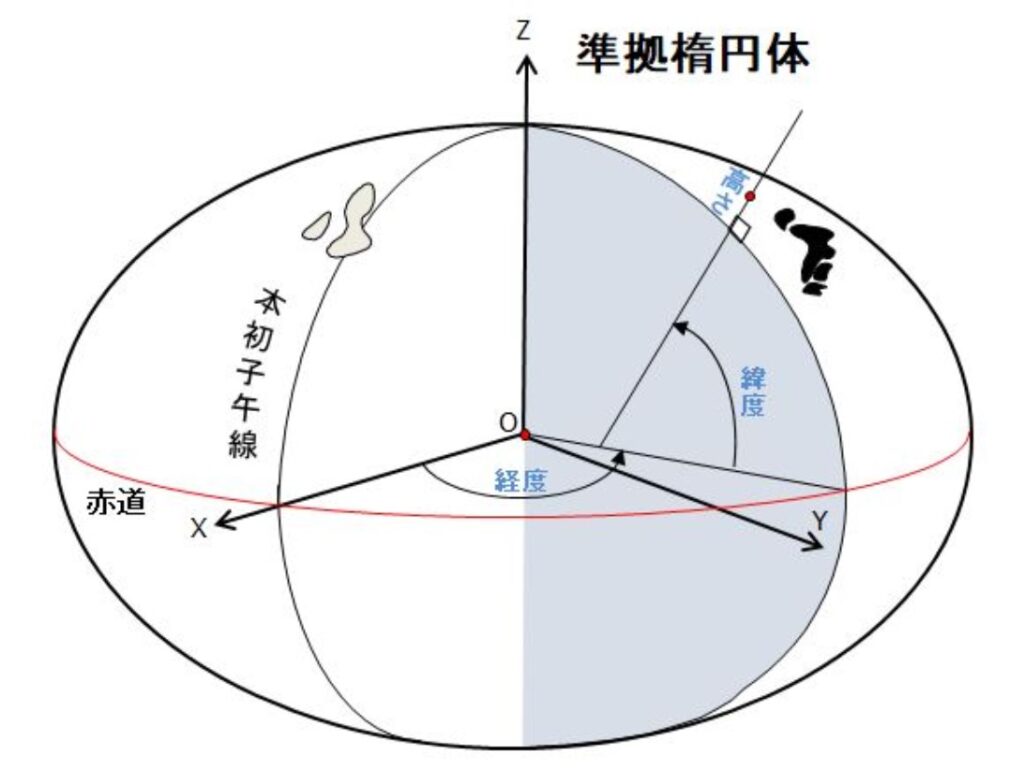
Z軸について考える

Z軸が一番考えやすいので先に検討します。
表より点Pは北緯0度から北緯60°へ動く。上記を踏まえると、0秒時点でZは0、100秒のときには少なくとも正の値を示すはずとわかる。
| 点名 | 緯度 | 経度 | 楕円体高 |
| A | 北緯 0°0’0” | 東経 135°0’0” | 0 m |
| B | 北緯 60°0’0” | 東経 135°0’0” | 0 m |
この時点で選択肢1,3,4に絞ることができる。
X軸について考える

「点AもBも東経135°だから値は一定」…と間違った考えに陥らないように!
表より点PはT=0~100のとき東経135°だから常に負の値であるとわかる。
点Pは北緯0度から北緯60°へ動く。北緯90°のときX軸の値は0であるから、徐々に値は0に近づいていく。
| 点名 | 緯度 | 経度 | 楕円体高 |
| A | 北緯 0°0’0” | 東経 135°0’0” | 0 m |
| B | 北緯 60°0’0” | 東経 135°0’0” | 0 m |
この時点で上記を満たすのは選択肢1のみである。

立体的に考えられるように、定期的に復習しましょう。
以上、正解は「選択肢1」でした。
↓令和4年測量士試験(午前) 解答解説↓
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 |
| 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 |
| 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士試験(午前)の過去問解説→記事一覧に飛びます。

コメント