試験問題の引用
令和４年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
測量士補試験の過去問演習ができるページがありますので、
フィードバックいただけると改善の参考にします。
第２５問 問題
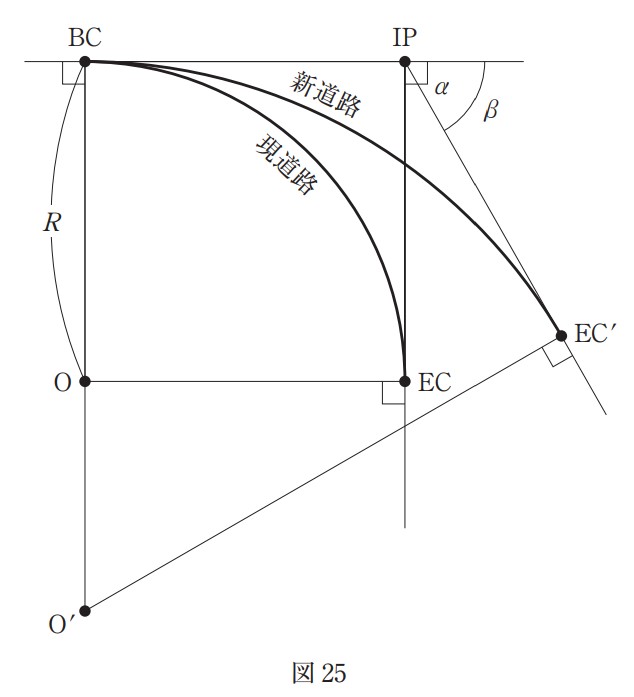
図 25 に示すように，曲線半径 R = 420 m，交角 a = 90°で設置されている，点 O を中心とする円曲線から成る現在の道路（以下「現道路」という。）を改良し，点 O’ を中心とする円曲線から成る新しい道路（以下「新道路」という。）を建設することとなった。
新道路の交角 b = 60°としたとき，新道路 BC ～ EC’ の路線長は幾らか。最も近いものを次の中から選べ。
ただし，新道路の起点 BC 及び交点 IP の位置は，現道路と変わらないものとし，円周率r = 3.14 とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
１．440 m
２．659 m
３．727 m
４．743 m
５．761 m
第２５問 解答・解説
正解は選択肢５です。以下、解説。
図を描きながら解いていきましょう。
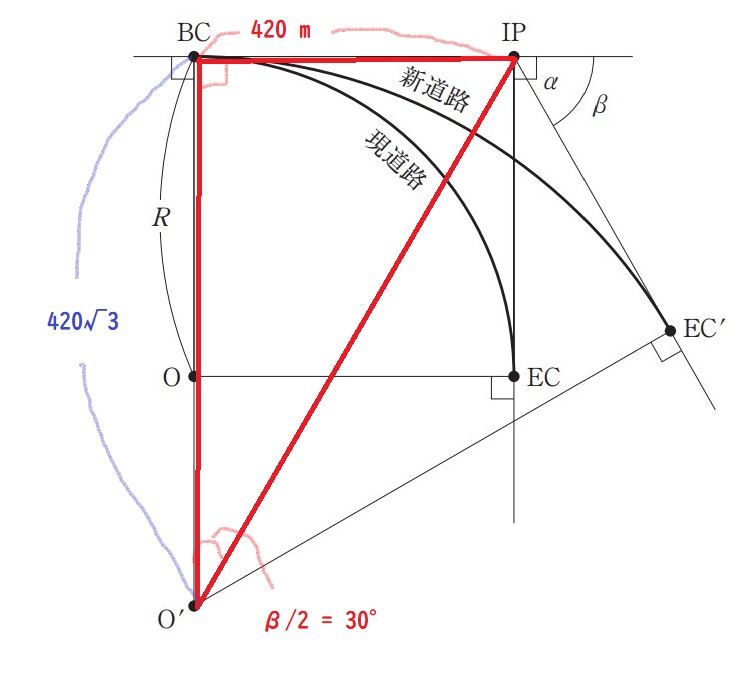
手順① 問題文で与えられている条件を図に記入
与えられている条件
曲線半径 R = 420 m，交角 a = 90°, 新道路の交角 b = 60°。
↓追記箇所を赤字で記載。
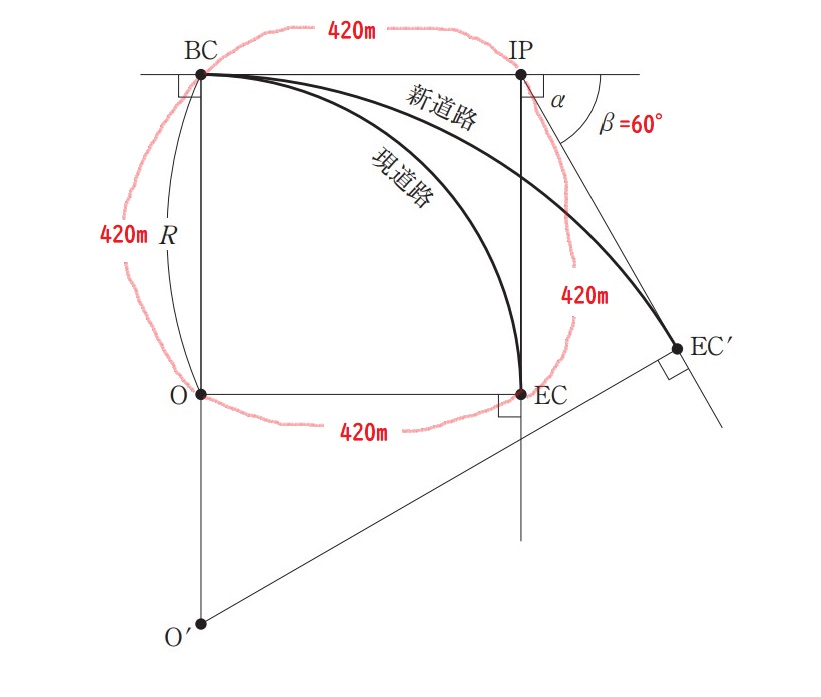
手順② 図形から読み取れる条件を図に記入
四角形の性質よりO’周りの角度もβであるとわかる。
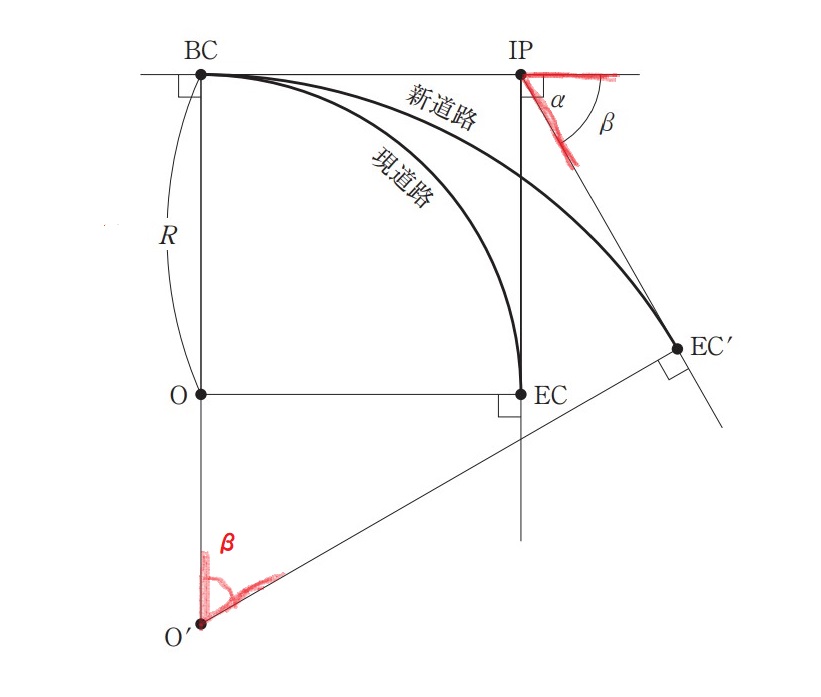
関係するところだけ抜き出すと下図のとおり。
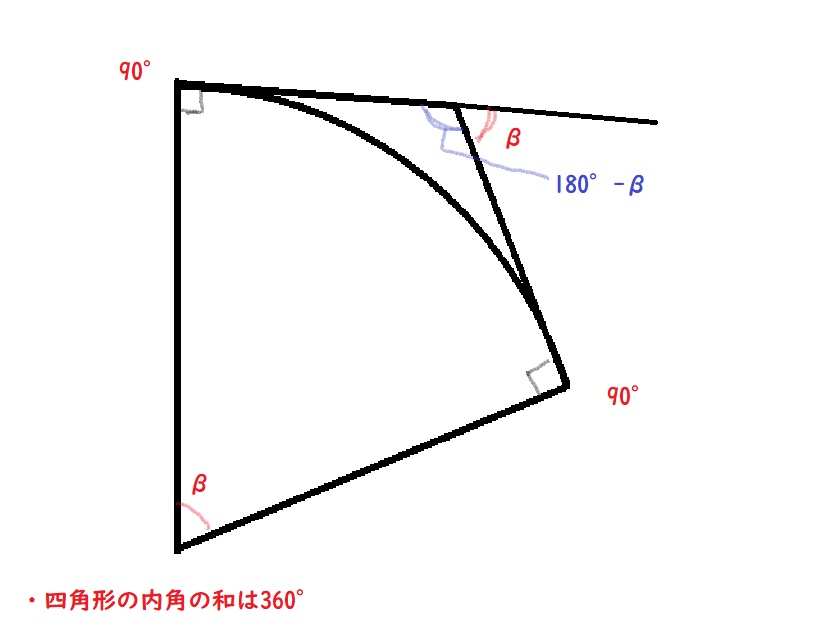
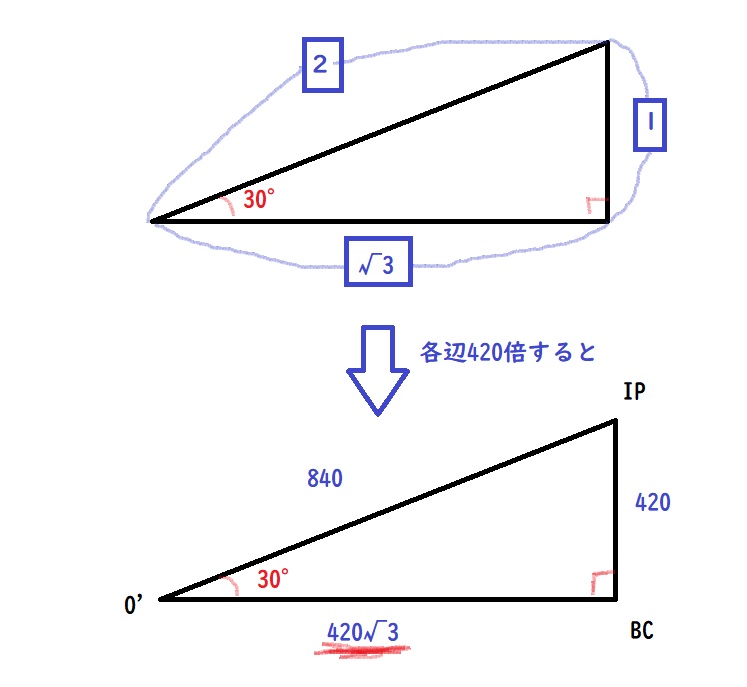
手順③ 補助線を引いて辺BC-O’の長さを求める
三角形の辺の比（下図参照）より辺BC-O’は
420√3=420×1.73205≒727.461
とわかる。
手順④ 新道路BC-EC’の路線長を求める
必要な情報だけ取り出して図にすると下のようになる。
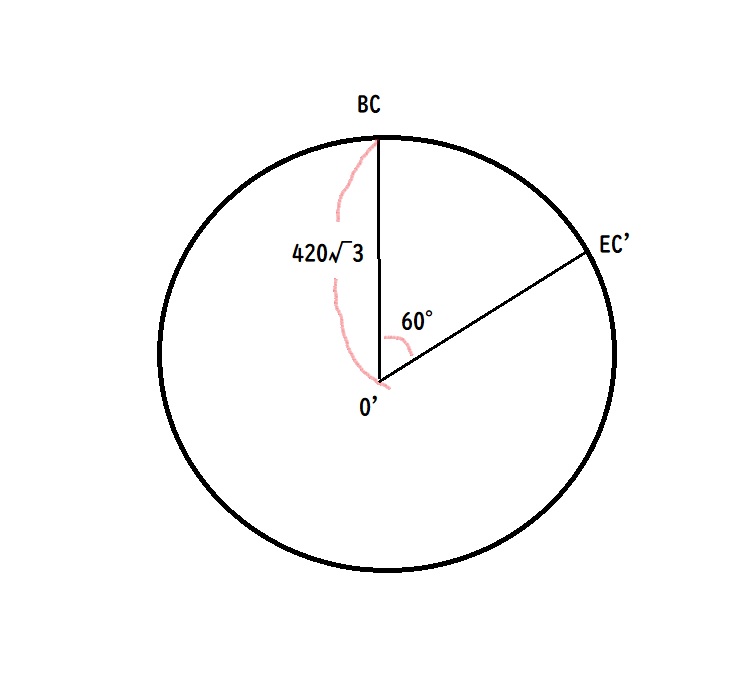
上記円の円周は
（直径）×（円周率）=(727.461 × 2) × 3.14=4568.455
よって求める路線長BC-EC’は
（円周）×60°/360°=4568.455×1/6=761.409
≒761 m
以上、正解は選択肢５です。
↓ほかの問題も見たい方はこちら↓
測量士補試験の過去問解説→記事一覧に飛びます。
令和3年測量士補試験の解説→令和3年測量士補試験第1問の解説記事に飛びます。
令和2年測量士補試験の解説→令和2年測量士補試験第1問の解説記事に飛びます。
測量士補試験におすすめのテキストについて→過去の記事に飛びます。
コメント
0.57735ではなく1.73205です。
あ様
ご指摘いただきありがとうございます。
内容を確認し、こちらの記載ミスとわかりましたので記載を修正いたしました。