試験問題の引用
令和4年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第8問 問題
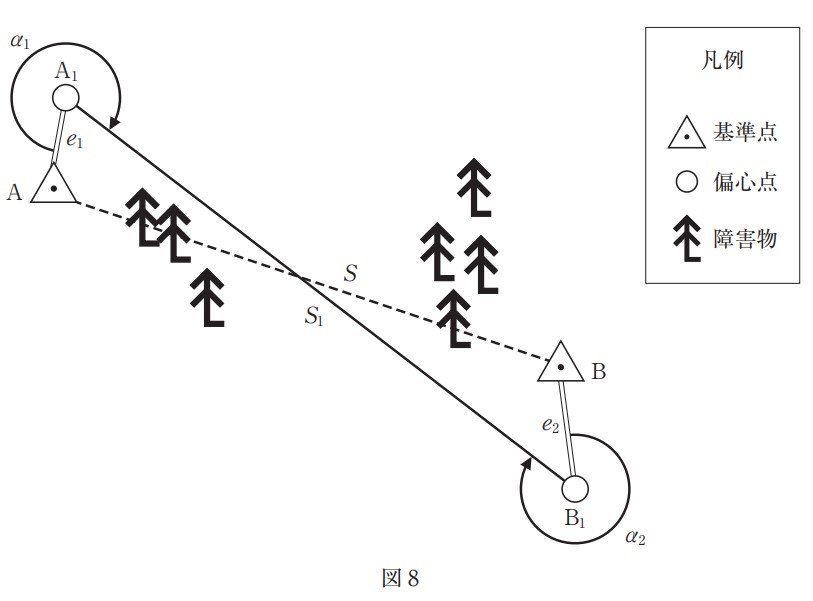
基準点 A,B 間の距離を測定しようとしたところ,障害物があったため,図 8 に示すように,それぞれ偏心点 A1,B1 に偏心して観測を行った。観測により得られた値は,表 8 のとおりである。このとき,基準点 A,B 間の基準面上の距離 S は幾らか。最も近いものを次の中から選べ。ただし,a1,a2 は偏心角,e1,e2 は偏心距離,S1 は偏心点 A1,B1 間の距離である。
また,距離は全て基準面上の距離に補正されているものとする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
| S1 | 1,000.000 m |
| e1 | 20.000 m |
| α1 | 300°00’00” |
| e2 | 50.000 m |
| α2 | 315°00’00” |
選択肢
1.953.190 m(≒√(908,571.35) m)
2.954.617 m(≒√(911,293.45) m)
3.954.644 m(≒√(911,346.12) m)
4.955.450 m(≒√(912,885.40) m)
5.956.097 m(≒√(914,120.89) m)
第8問 解答・解説
正解は選択肢5です。
以下、解説。
「相互偏心の計算」の式を使う
偏心補正の計算では、作業規程の準則の「付録6 計算式集」の「基準点測量の部」の「2.3.3の相互偏心の計算」の式を使用する。
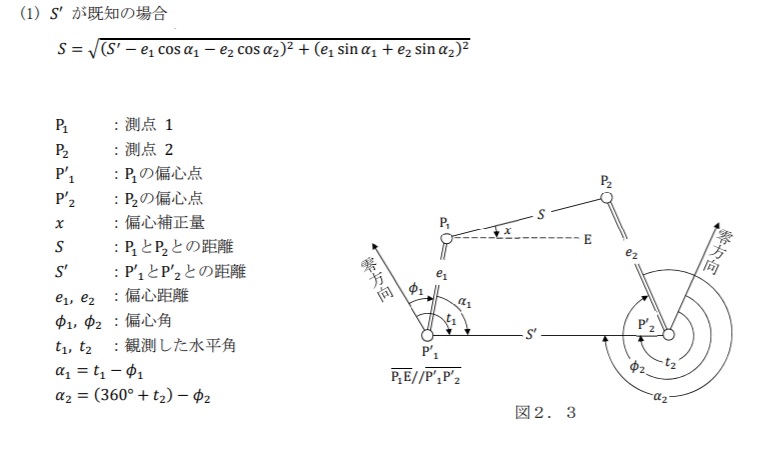
答えを求める

公式に値を代入して答えを求める。
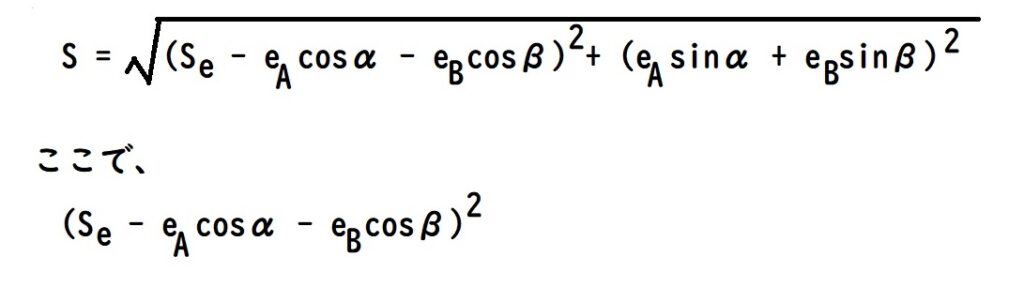
= (1000.000 – 20.000 × cos300° – 50.000 × cos315°)2
= (1000.000 – 20.000 × 0.50000 – 50.000 × 0.70711)2
= (954.6445)2
さらに
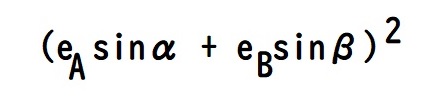
= (20.000 × sin300° + 50.000 × sin315°)2
= (20.000 × (-0.86603) + 50.000 × (-0.70711))2
= (-52.6761)2
よって
S = √((954.6445)2 + (-52.6761)2)
=√(914120.8929)
ゆえに正解は「選択肢5」。
別解:正弦定理と余弦定理で解く
正弦定理とは?
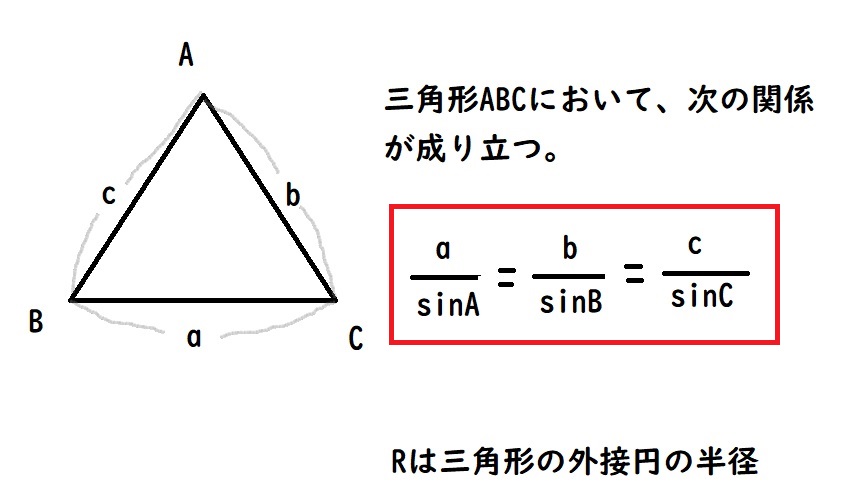
余弦定理とは?
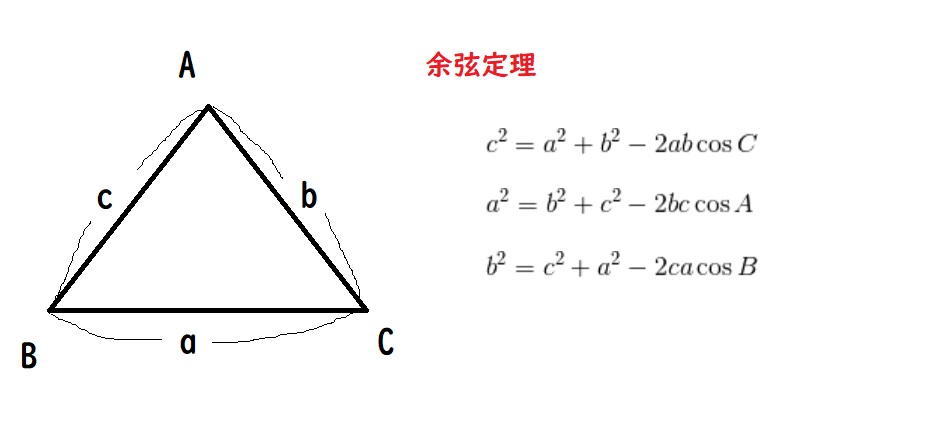
解き方
問題文を簡易的に図示すると下のようになる。
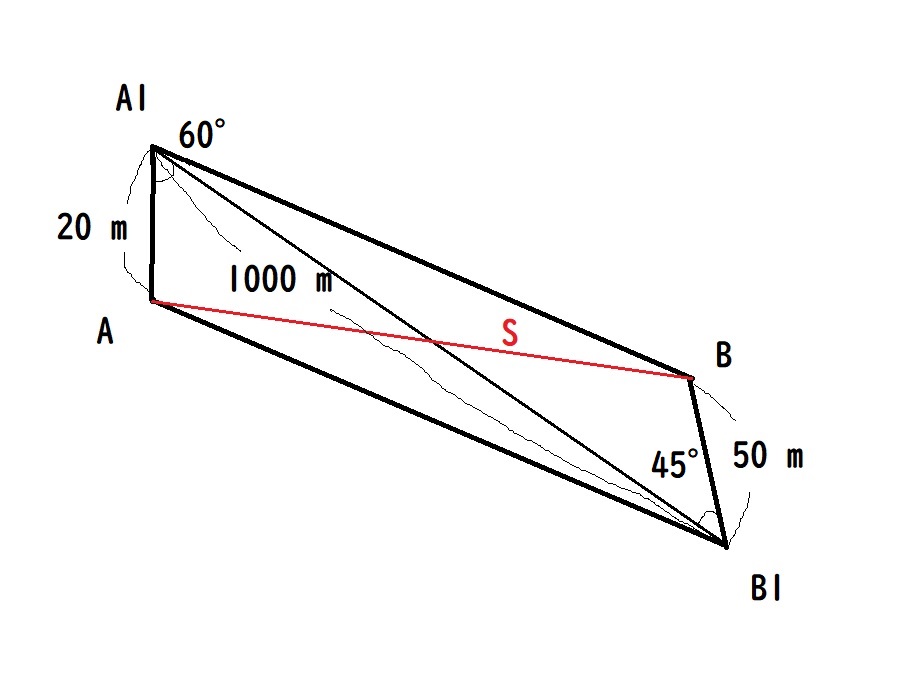
手順① 三角形A1 A B1に注目


上図から辺A B1は余弦定理で、∠A B1 A1は正弦定理で求められる…と見通しがつきます。
余弦定理より
(辺A B1)2 = 202 + 10002 – 2×20×1000×cos60°
= 400 + 1000000 -40000 × 0.5000
= 1000400 – 20000 = 980400
(辺A B1) = √(980400)
正弦定理より
sin∠A B1 A1 =20 × sin60° / √(980400)
=20 × 0.86603 / √(980400)
=0.01749
関数表より∠A B1 A1は1度とわかる。
手順② 三角形A1 A Bに注目してSを求める
手順①でわかった情報を図に書き込むと下記のとおり。
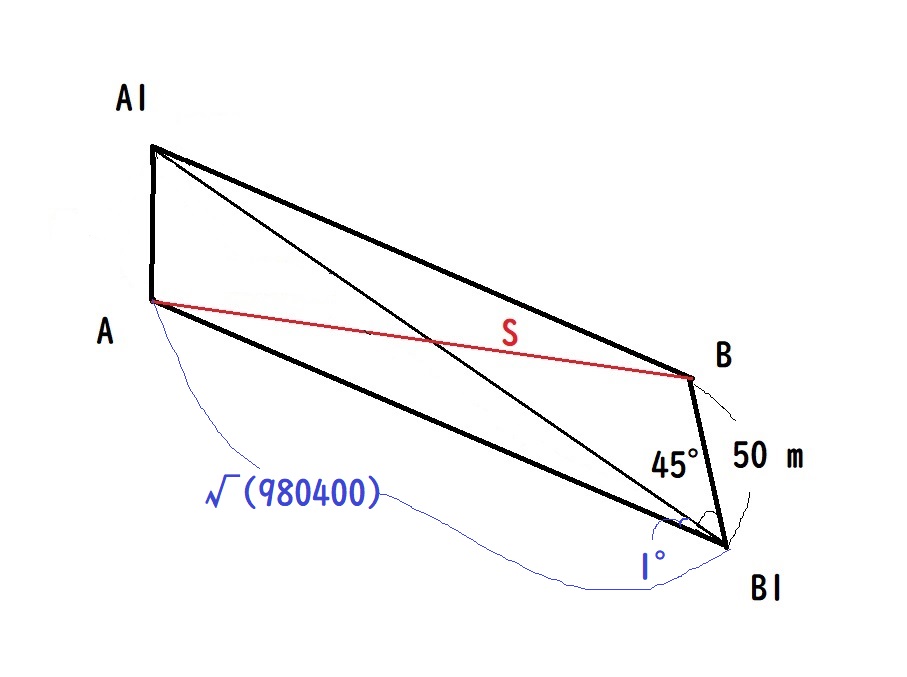
三角形A1 A Bのみに着目すると下図のとおり。
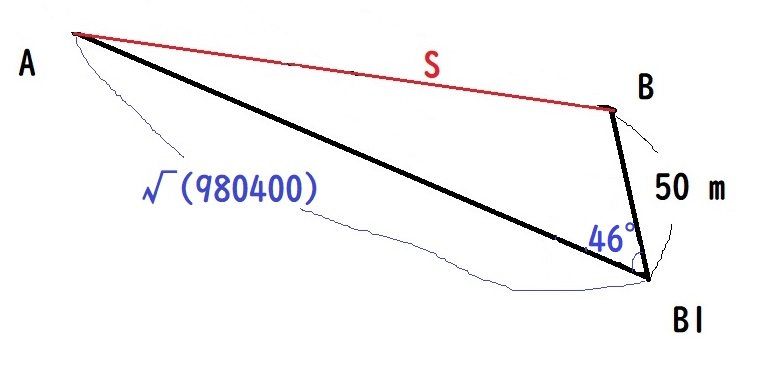

余弦定理を使えばSの長さがわかりそうですね
余弦定理より
S2 = 502 + (√(980400))2 – 2×50×√(980400)×cos46°
= 2500 + 980400 -100 × 990.15 × 0.69466
= 982900 – 68782 = 914118
S = √(914118)
よって、近い値である「選択肢5」が正解でした。
どうしても計算問題が苦手な方へ おすすめしたいアガルートの有料講座(税込27,280円)
⇒測量士試験|パターンで攻略!計算問題
↓令和4年測量士試験(午前) 解答解説↓
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 |
| 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 |
| 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士試験(午前)の過去問解説→記事一覧に飛びます。

コメント