試験問題の引用
令和4年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第5問 問題
100 点を満点とするある試験において,受験者の点数の分布が近似的に平均 60 点,標準偏差10 点の正規分布に従うことが分かった。この試験は 1,000 人が受験し,上位 3 % が合格する。この試験の最低合格点は幾らか。最も近いものを次のページの中から選べ。
ただし,必要に応じて表 5 の値を用いよ。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
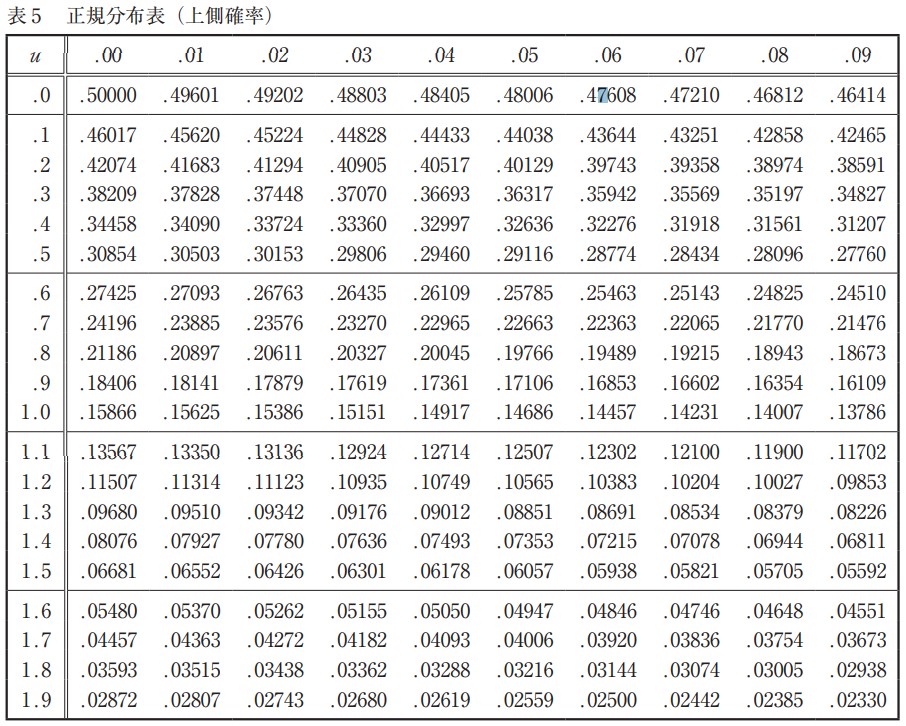
表5は u = 0.00 ~ 1.99 に対する,標準正規分布の正規分布表(上側確率)である。
また,標準正規分布の確率密度関数 f(x)の上側確率 Q(u)は式 5 で表される。
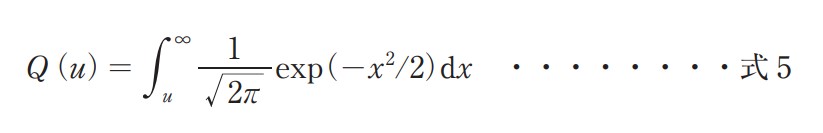
これは図 5 の着色部の面積にあたる。
例 :u = 1.23 に対する上側確率 Q(u)は,表 5 の左の見出しから小数第 1 位までの 1.2 と,上の見出しから小数第 2 位の .03 とが交差するところで,Q(u)= 0.10935 が得られる。

選択肢
1.74点
2.79点
3.84点
4.89点
5.94点
第5問 解答・解説
正解は選択肢2です。

標準偏差は近年頻出です。
以下、解説。
理屈はわかりませんがこの解き方で解けます

上位3%ということはQ(U)の面積部分が3%になるときを考えればよいと見当がつきます。
上位3%に相当するのは正規分布表(上側確率)において0.03となるところ。
表5において一番0.03に近いuの値は1.88。

したがって、求める点数は
(求める点数)=u×(標準偏差)+(平均値)
=1.88×10+60
=78.8
選択肢のうち最も値の近い79、選択肢2が正解である。
以上、正解は「選択肢2」でした。
どうしても計算問題が苦手な方へ おすすめしたいアガルートの有料講座(税込27,280円)
⇒測量士試験|パターンで攻略!計算問題
↓令和4年測量士試験(午前) 解答解説↓
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 |
| 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 |
| 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士試験(午前)の過去問解説→記事一覧に飛びます。

コメント