試験問題の引用
令和4年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第25問 問題
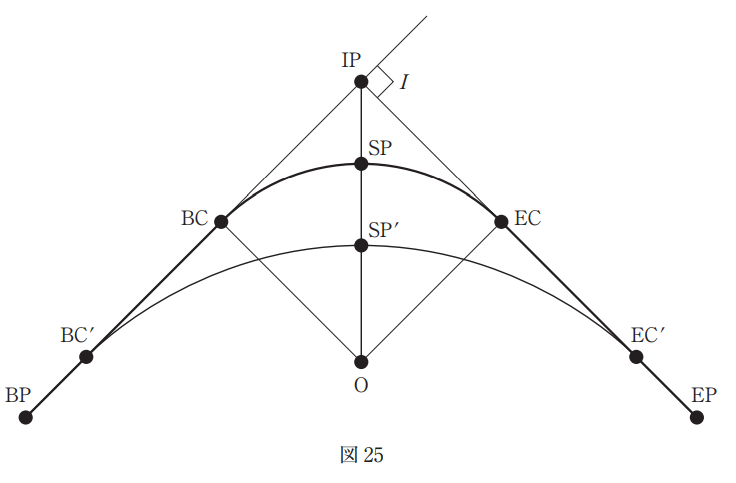
図 25 のように,直線部分 BP ~ BC,円曲線始点 BC,円曲線終点 EC,点 O を中心とする円曲線部分 BC ~ EC 及び直線部分 EC ~ EP から構成される道路を計画した。
ところが,曲線中点 SP 付近に歴史的な埋設物が発見された。交点 IP,起点 BP,終点 EP の位置,交角 I は変更せず,円曲線始点 BC’ ,円曲線終点 EC’ ,点 SP から点 O 方向に 40 m 移動
させた点 SP’ を曲線中点とする円曲線 BC’ ~ EC’ に設計変更したい。設計変更前の道路 BP ~SP ~ EP の距離と,設計変更後の道路 BP ~ SP’ ~ EP との距離の差の絶対値は幾らか。最も近
いものを次の中から選べ。
ただし,設計変更前の円曲線半径 R = 100 m,交角 I = 90°,直線部分 BP ~ BC 及び EC ~ EPの距離はそれぞれ 140 m,円周率 r = 3.142 とする。
なお,関数の値が必要な場合は,巻末の関数表を使用すること。
選択肢
1.41 m
2.63 m
3.85 m
4.97 m
5.152 m
第25問 解答・解説
正解は選択肢1です。

最近の過去問では見かけない問題です。
平成22年の測量士試験(午後)にて類題の出題があります。
以下、解説。
手順1 図にわかっている数字を書き込む
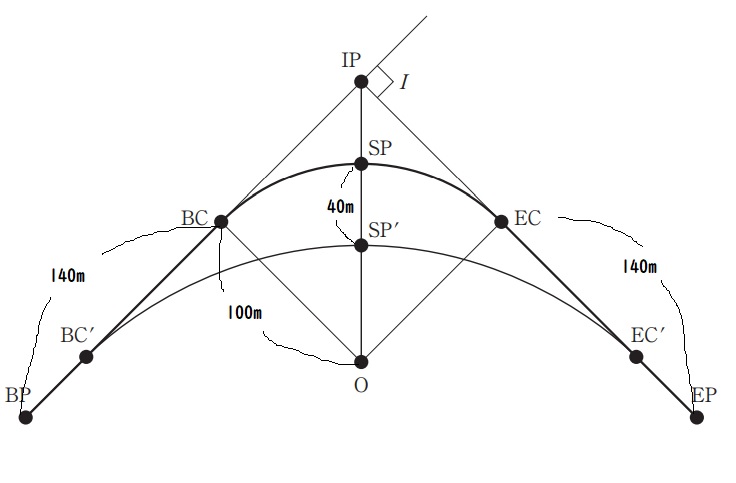
交点IPが90°であることから四角形IP-EC-O-BCは正方形とわかります。
手順2 公式から答えを求める
辺IP-SPをSLとおく。また辺IP-SP’をSL’とすると
SL= 100√2 – 100 = 100 × 1.41421 -100 ≒ 41.4
SL’= 41.4 + 40 = 81.4
ここで曲線BP-SP’-EPの半径をR’とする。
R’= SL’ / (( 1 / cos(90°/2)) -1)
= SL’ / ((1 / cos45°) -1)
= 81.4 / ( 1.414 -1 ) = 196.6 m
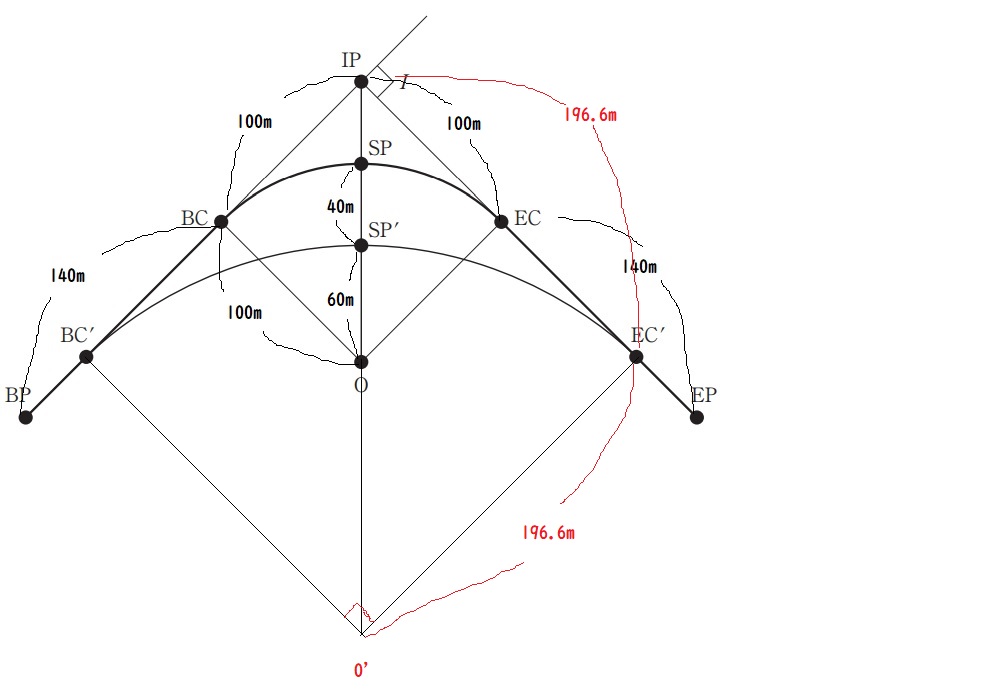
BP-BC’ = 100+ 140 – 196.6 = 43.4
手順3 距離の差の絶対値を求める
・設計変更前の道路 BP ~SP ~ EP の距離
140 × 2 + (1/4 × 2×3.14×100 )= 437
・設計変更後の道路 BP ~ SP’ ~ EPの距離
43.4 × 2 +(1/4 × 2×3.14×196.6 ) = 395.5
よって求める経路差は
437 – 395.5 = 41.5
以上、正解は「選択肢1」でした。
どうしても計算問題が苦手な方へ おすすめしたいアガルートの有料講座(税込27,280円)
⇒測量士試験|パターンで攻略!計算問題
↓令和4年測量士試験(午前) 解答解説↓
| 第1問 | 第2問 | 第3問 | 第4問 | 第5問 | 第6問 | 第7問 |
| 第8問 | 第9問 | 第10問 | 第11問 | 第12問 | 第13問 | 第14問 |
| 第15問 | 第16問 | 第17問 | 第18問 | 第19問 | 第20問 | 第21問 |
| 第22問 | 第23問 | 第24問 | 第25問 | 第26問 | 第27問 | 第28問 |
測量士試験(午前)の過去問解説→記事一覧に飛びます。

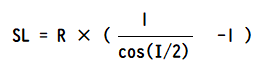
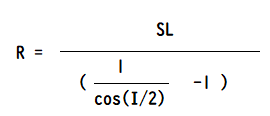
コメント