試験問題の引用
令和4年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第１３問 問題
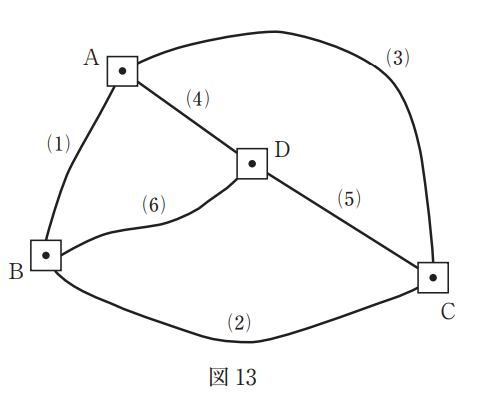
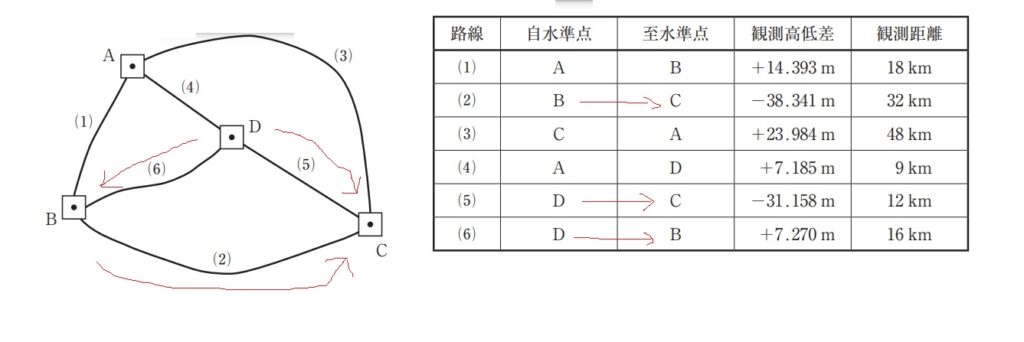
図 13 に示す水準点 A ～ D において，⑴ ～ ⑹ の路線で水準測量を行い，表 13 の観測高低差を得た。環閉合差を点検した結果から判断して，再測すべき路線として最も適当なものはどれか。次の中から選べ。
ただし，環閉合差の許容範囲は 5 mm √S （S は観測距離，km 単位）とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
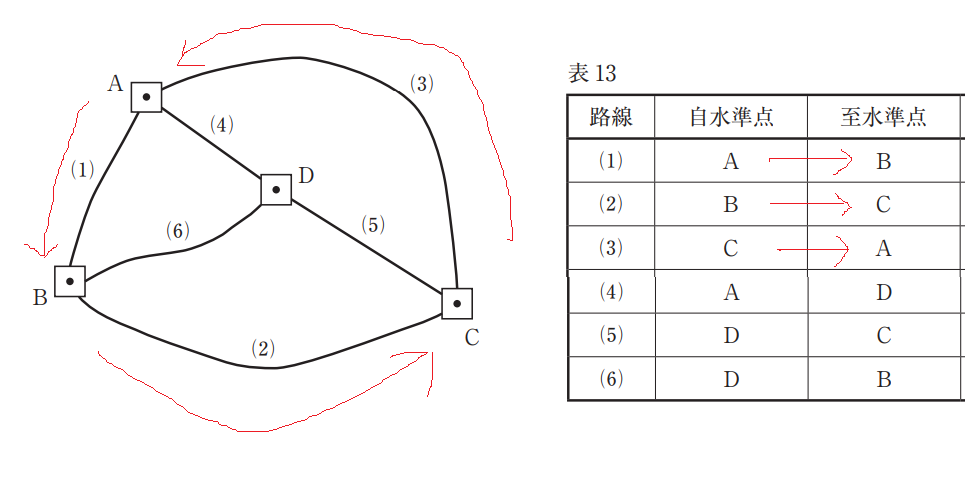
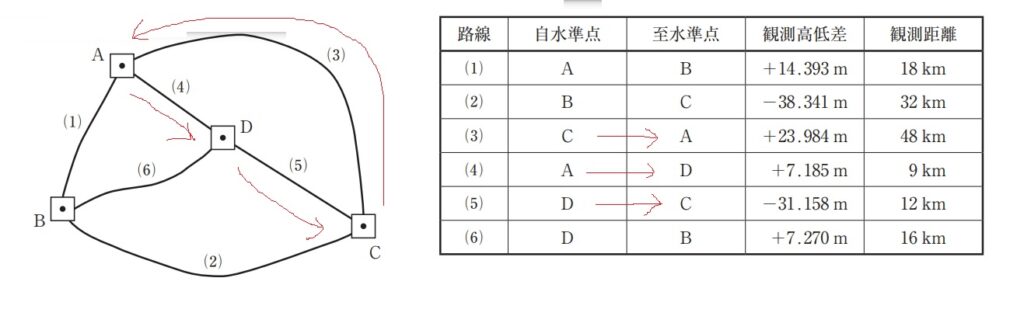
| 路線 | 自水準点 | 至水準点 | 観測高低差 | 観測距離 |
| (1) | A | B | +14.393 m | 18 km |
| (2) | B | C | -38.341 m | 32 km |
| (3) | C | A | +23.984 m | 48 km |
| (4) | A | D | +7.185 m | 9 km |
| (5) | D | C | -31.158 m | 12 km |
| (6) | D | B | +7.270 m | 16 km |
選択肢
１．路線(1)
２．路線(2)
３．路線(4)
４．路線(5)
５．路線(6)
第１３問 解答・解説
正解は選択肢５です。
類題は平成28年問12にて出題されています。
以下、解説。
1.各環での許容閉合差を求める
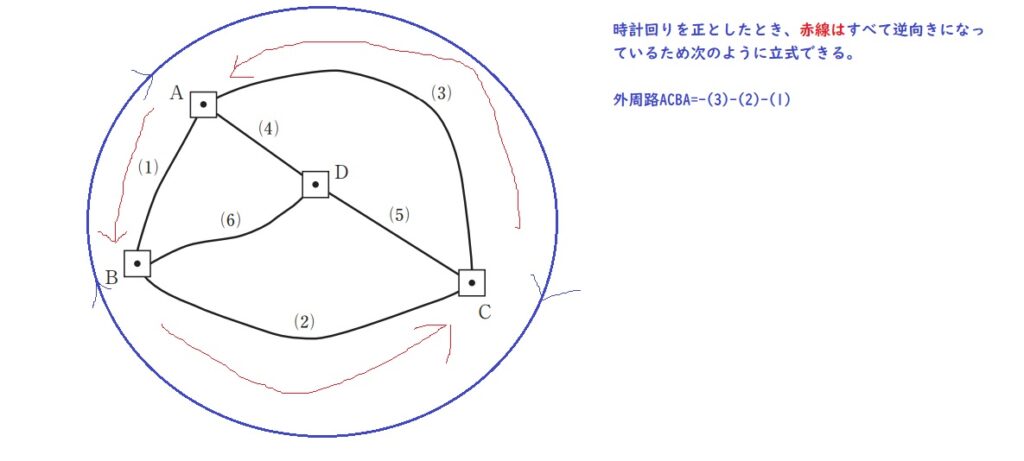
①外周路(路線1,2,3)について閉合差
5√(18+32+48) = 5√98 = 5×9.89949 ≒ 49.5
②右上環(路線3,5,4)について閉合差
5√(48+12+9) = 5√69 = 5×8.30662 ≒ 41.5
③下環(路線2,6,5)について閉合差
5√(32+16+12) = 5√60 = 5×7.74597 ≒ 38.7
④左上環(路線1,4,6)について閉合差
5√(18+9+16) = 5√43 = 5×6.55744 ≒ 32.8
2.各環での閉合差を求める
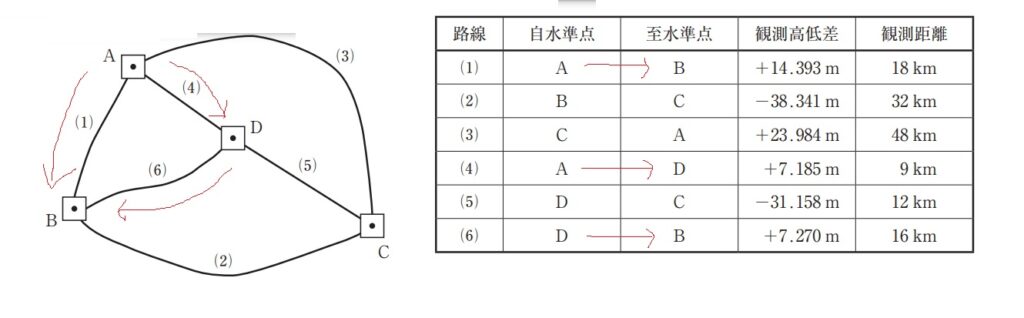
表13の路線の方向に注意しながら、立式しましょう。
各環の時計回りでの閉合差を計算する。
①外周路について閉合差
-(3)-(2)-(1)=-23.984 -(-38.341) -14.393
= -0.036 m = -36 mm
なぜ -(3)-(2)-(1) という立式にしたのか
表13をもとに路線(1),(2),(3)がどの点からどの点に向かって測量したのか、測量の進行方向を赤線で示すと下図のとおり。
立式する際には、数学のベクトルと同じ考え方です。
きちんと矢印の方向が一周するように立式できれば問題ありません。
今回は時計回りを正としたので、A→C→B→Aの順になるように符号をつけていきます。
A→Cとするには-(3)
C→Bとするには-(2)
B→Aとするには-(1)
ゆえに-(3)-(2)-(1)と立式しています。（赤線がすべて反時計回りのためすべてマイナスの符号とも言い換えられます）
立式の順番に決まりはありませんが、きちんと環になるように設定しましょう。
符号はそれぞれの環内で時計回りか否かで決まります。
②右上環について閉合差
-(3)-(5)-(4)=-23.984 -(-31.158) -7.185
=-0.011 m = -11 mm
表13をもとに路線(3),(5),(4)がどの点からどの点に向かって測量したのか、測量の進行方向を赤線で示すと下図のとおり。
いずれの路線も反時計回りのため、-(3)-(5)-(4)と立式。
③下環について閉合差
-(2)-(6)+(5)= -(-38.341) -7.270 -31.158
= -0.087 m = 87 mm
表13をもとに路線(2),(6),(5)がどの点からどの点に向かって測量したのか、測量の進行方向を赤線で示すと下図のとおり。
赤線が時計周りなのは路線(5)のみ。よって-(2)-(6)+(5)と立式。
④左上環について閉合差
-(1)+(4)+(6)= -14.393 +7.185 +7.270
= 0.062 = 62 mm
表13をもとに路線(1),(4),(6)がどの点からどの点に向かって測量したのか、測量の進行方向を赤線で示すと下図のとおり。
赤線が時計周りなのは路線(4),(6)のみ。よって-(1)+(4)+(6)と立式。
3. 1,2の計算結果を基に再測すべき路線を選ぶ
許容閉合差より閉合差が大きいものは再測すべき路線が含まれているとわかる。
| 許容閉合差 | 閉合差(絶対値) | 再測の要・不要 | |
| 外周路 | 49.5 | 36 | 不要 |
| 右上環 | 41.5 | 11 | 不要 |
| 下環 | 38.7 | 87 | 要 |
| 左上環 | 32.8 | 62 | 要 |
上記にて再測が不要と判断された「外周路」、「右上環」は路線(1),(2),(3),(4),(5)である。
よって、再測すべきは上記に含まれない路線(6)とわかる。
ゆえに正解は「選択肢５」。
令和4年測量士試験の解説は随時更新予定です。
↓ほかの問題も見たい方はこちら↓
測量士試験（午前）の過去問解説→記事一覧に飛びます。
コメント
こんにちは いつも大変勉強になります。
各環の時計回りでの閉合差を計算するの後の計算式の立式が理解できなくて困ってい
ます。
①外周路について閉合差 この計算をする場合1-3-2の順ではないのですか？
また符号のつけ方に何か法則性があるのでしょうか。
ぞぞ様
ご質問いただきありがとうございます。
記事中に解説を追加しましたのでご確認ください。
質問への回答をします。
＞外周路について閉合差 この計算をする場合1-3-2の順ではないのですか？
時計回りを正としていますので、水準点A→C→B→Aの順になるように立式しています。
＞また符号のつけ方に何か法則性があるのでしょうか。
今回、時計回りを正と設定しています。
それぞれの環ごとで時計回りの向きで測量していれば正、反時計回りの向きであれば負の符号をつけいています。
いつも勉強させていただいております。
環閉合差の許容範囲についてですが
④左上環(路線1,4,6)について閉合差に関しては
5√(18+16+9) = 5√43 = 5×6.55744 ≒ 32.8
が正しいと思います。それによって結果は変わらないのですが
ご確認いただければと思います。
めーてる様
ご指摘いただきました箇所について、内容確認いたしました。
ご指摘の通り記事が誤りでしたので、数字を修正させていただきました。
コメントにて教えていただき誠にありがとうございました。