試験問題の引用
令和3年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
第15問 問題
図 15 のように、高低差 Z を求めるために、トータルステーションを用いて、放射法により既知点Aから求点Bを観測した。
次の文は、求めた高低差 Z の標準偏差を計算する過程を示したものである。 ア 〜ウ に入る語句の組合せとして最も適当なものはどれか。
求点 B の高低差 Z は、既知点Aから求点Bの斜距離 D 及び高低角 θ を使うと、式 15−1で表される。ただし、θ の単位はラジアンとする。
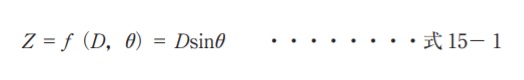
ここで、斜距離 D、高低角 θ それぞれの観測値の標準偏差を σD、σθ とした場合の、高低差 Zの標準偏差 σZ を求めることにする。
斜距離 D と高低角 θ の観測が互いに独立であれば、それぞれの観測値の分散を σD2、σθ2 とした場合、両者の共分散は 「 ア (0 or 1)」 となる。このとき、高低差 Z の分散 σZ2 は、誤差伝播の法則から式 15−2で求められる。
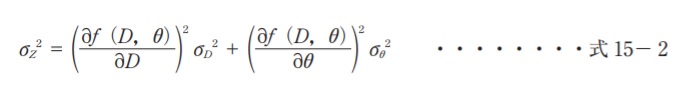
ここで、式 15−1を D 及び θ で偏微分すれば、
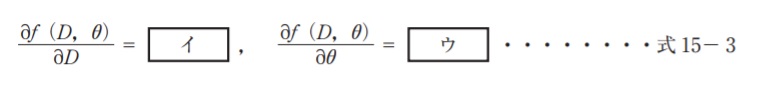
となる。式 15−2及び式 15−3から、標準偏差 σZ は式 15−4で求まる。

「 イ(sinθ or cosθ)」 、 「 ウ(Dsinθ or Dcosθ)」
選択肢
| ア | イ | ウ | |
| 1. | 0 | sinθ | Dsinθ |
| 2. | 1 | cosθ | Dsinθ |
| 3. | 0 | sinθ | Dcosθ |
| 4. | 1 | sinθ | Dsinθ |
| 5. | 0 | cosθ | Dsinθ |
第15問 解答・解説
正解は選択肢3です。
ア
0
斜距離 D と高低角 θ の観測が互いに独立であれば、それぞれの観測値の分散を σD2、σθ2 とした場合、両者の共分散は 「 ア (0 or 1)」 となる。
共分散について、他サイトから引用して解説します。
共分散の符号の意味
共分散は,「X の偏差 × Y の偏差」の平均なので
高校数学の美しい物語
共分散が大きい(正)→ X が大きいとき Y も大きい傾向がある
共分散が 0 に近い→ X と Y にあまり関係はない
共分散が小さい(負)→ X が大きいとき Y は小さい傾向がある
今回の問題では、 「斜距離 D と高低角 θ の観測が互いに独立 」とした場合を聞かれていますので、共分散は0ということになります。
イ、ウ
イ sinθ, ウ Dcosθ
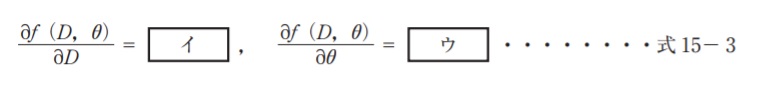
イを求めるには、DsinθをDで偏微分すればよい。
DsinθをDで偏微分すると1×sinθ=sinθ
ウを求めるには、 Dsinθをθで偏微分すればよい。
Dsinθをθで偏微分 するとD×cosθ=Dcosθ
統計、微分の知識がない場合は捨て問にしてもいいかもしれません。
正解は「選択肢3」
どうしても計算問題が苦手な方へ おすすめしたいアガルートの有料講座(税込27,280円)
⇒測量士試験|パターンで攻略!計算問題
↓令和3年測量士試験(午前) 解答解説↓

コメント