標準偏差が何か理解して解きましょう
問題
ある試験において、受験者の点数の平均が60点、標準偏差が10点の結果を得た。受験者の点数の分布が、近似的に平均μ、標準偏差σの正規分布に従うと仮定した場合、80点以上90点以下の人の割合は幾らか。
ただし、正規分布の性質から、μ±σの範囲に入る確率は68.3%、μ±2σの範囲に入る確率は95.5%、μ±3σの範囲に入る確率は99.7%とする。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
選択肢
１．0.3%
２．2.1%
３．2.3%
４．4.2%
５．4.5%
解答
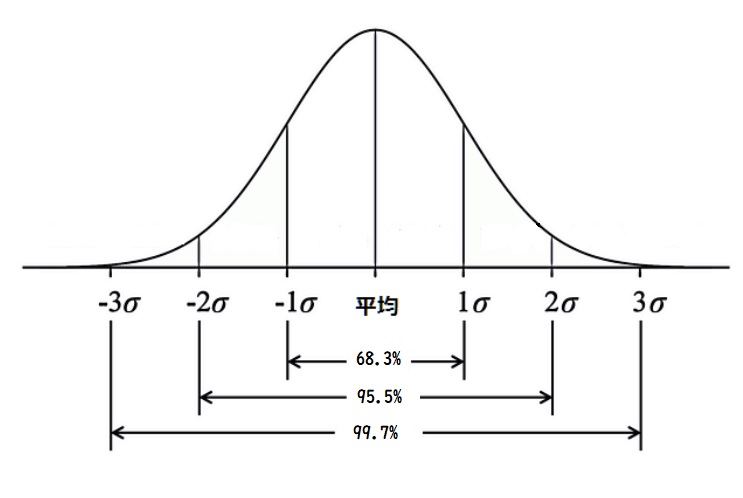
問題文より平均点μ＝60点、
標準偏差σが10点ということから、
μ±σ＝50～70点。
μ±2σ＝40〜80点。
μ±3σ＝30〜90点。
80～90点の人を求めるために
①30～40点、80～90点の割合を求める
②80～90点の人の割合は①を2で割って求める（正規分布の性質を利用）
①99.7%-95.5%=4.2%
②4.2%÷2＝2.1%
よって正解は選択肢2でした。
↓令和２年測量士試験（午前） 解答解説↓
コメント