問題
〔No. 27〕
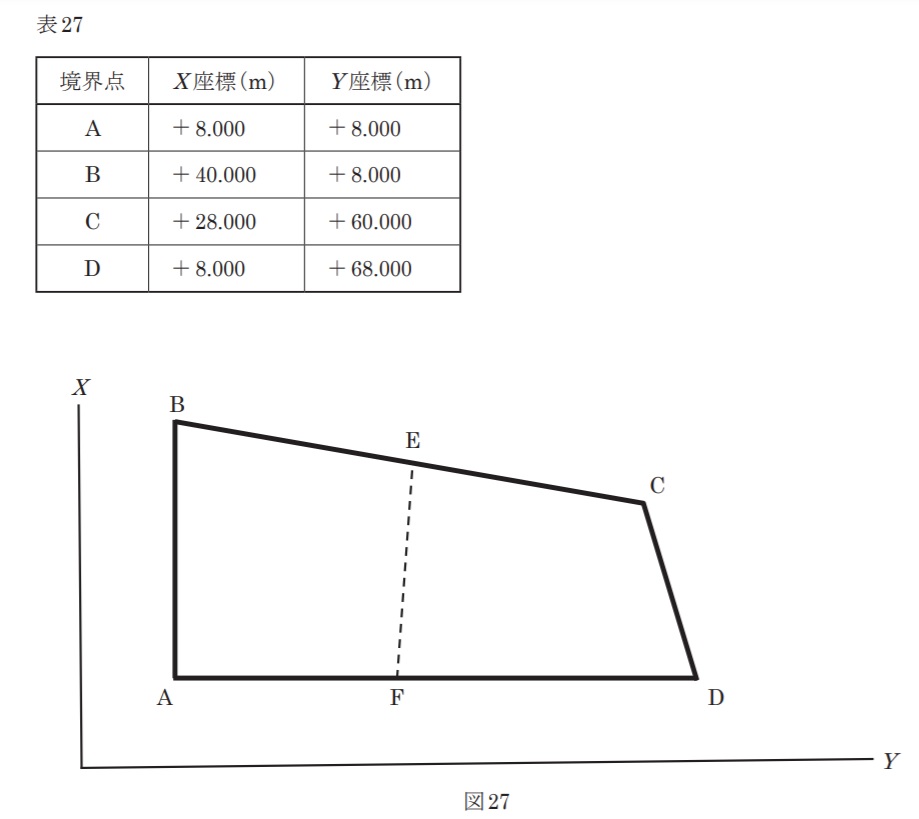
表27は，面積 1,432.000 m2 の四角形ABCDの土地を構成する各境界点の平面直角座標系（平成14年国土交通省告示第 9 号）に基づく座標値を示す。公共測量によって，この土地を図27で示すように，面積の等しい四角形ABEF及びFECDの 2 つの土地に分割したい。
点EをBE＝ECとなる位置に設置したとき，点FのY 座標値は幾らか。最も近いものを次の中から選べ。
なお，関数の値が必要な場合は，巻末の関数表を使用すること。
選択肢
1． ＋27.629 m
2． ＋29.351 m
3． ＋31.077 m
4． ＋33.357 m
5． ＋37.000 m
解答
正解は選択肢３です。
ステップ① 点Eの座標を求める
問題文よりBE=ECであるから、
点Eの座標は
X座標：28 +（40 – 28）/ 2 = 34
Y座標：8 + (60 – 8 ) / 2 =34
よって、E（34,34）
ステップ② 座標法により計算
下表を作るための計算手順を覚えましょう
①Y座標に関して（Yn+1-Yn-1）を計算する。
②①にX座標値を掛け算する。（(Yn+1-Yn-1)×Xn）
③各境界点ごとの②をすべて足し合わせ、２で割る。四角形の面積が算出される。
| 境界点 | X座標（ｍ） | Y座標（ｍ） | Yn+1-Yn-1 | (Yn+1-Yn-1)×Xn |
| A | +8.000 | +8.000 | 8-Y | (8-Y)×8 = 64-8Y |
| B | +40.000 | +8.000 | 34-8=26 | 26×40 = 1040 |
| E | +34.000 | +34.000 | Y-8 | (Y-8)×34 = 34Y -272 |
| F | +8.000 | Y | 8-34=-26 | -26×8 = –208 |
| 合計÷2 | (26Y+624)÷2 =13Y+312 |
問題文より四角形ABEFの面積は
1432.00÷2=716.00
よって、次の等式が成り立つ
13Y + 312 = 716
13Y = 404
Y = 31.0769
以上より点FのY座標は31.077
正解は選択肢「３」です。
↓令和２年測量士試験（午前） 解答解説↓
コメント