試験問題の引用
令和４年の試験問題は国土地理院HPから引用しています。
https://www.gsi.go.jp/LAW/SHIKEN/past.html
測量士補試験の過去問演習ができるページがありますので、
フィードバックいただけると改善の参考にします。
第７問 問題
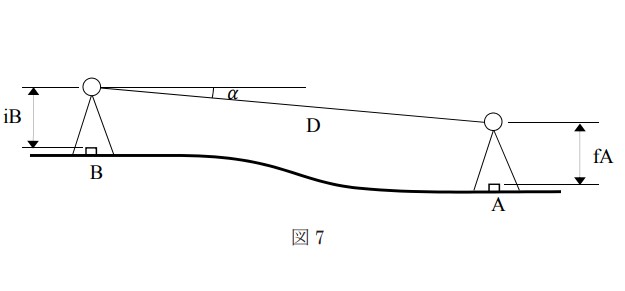
図7は、トータルステーションによる偏心観測について示したものである。図 7 のように、既知点 B において、既知点 A を基準方向として新点 C 方向の水平角を測定しようとしたところ、既知点 B から既知点 A への視通が確保できなかったため、既知点 A に偏心点 P を設けて、水平角 T ‘、偏心距離 e 及び偏心角U の観測を行い、表 7 の結果を得た。このとき、既知点 A 方向と新点 C 方向の間の水平角 T は幾らか。最も近いものを次の中から選べ。
ただし、既知点 A、B 間の距離 S は、1,500 m であり、S 及び e は基準面上の距離に補正されているものとする。
また、角度 1 ラジアンは，（2 × 105）” とする。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
| Φ | 210°00’00” |
| e | 2.70 m |
| T’ | 50°41’00” |
１．50°30’00”
２．50°32’00”
３．50°34’00”
４．50°36’00”
５．50°38’00”
第７問 解答・解説
正解は選択肢5です。以下、解説。
頻出問題ですから、しっかり解く手順を覚えましょう。
手順１ わかりやすく図示する
水平角Tをもとめるためには下図に示した角度xがわかればよい。
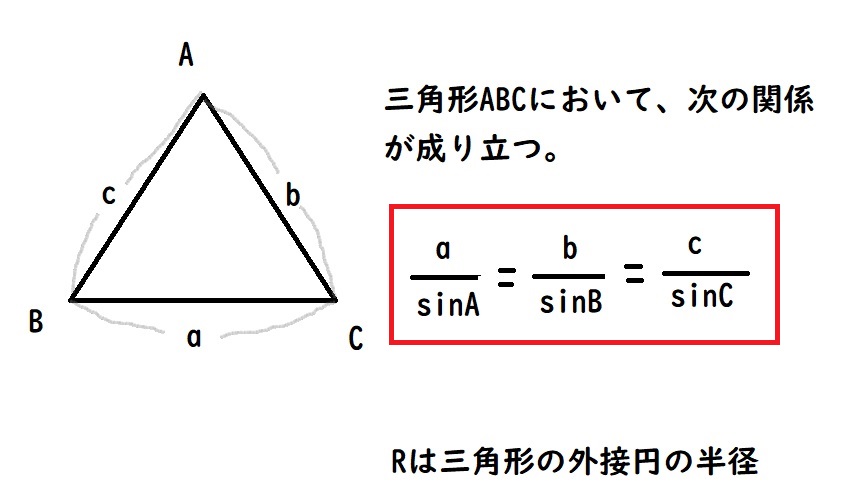
上図より正弦定理が使えることがわかります。
手順２ 計算する
正弦定理より
(1500 m /sin150°) = (2.7 m / sinx )
sinx = 2.7 × sin30° ÷ 1500
= 2.7 × 0.50 ÷1500
= 0.0009（ラジアン）
ここで、問題文「角度 1 ラジアンは，（2 × 105）” とする」より
角度x =0.0009 × （2 × 105）”
=180” = 3’00”
よって、求める水平角Tは
T = 50°41’00” – 3’00”
= 50°38’00”
以上、正解は選択肢5です。
補足 正弦定理とは？
↓ほかの問題も見たい方はこちら↓
測量士補試験の過去問解説→記事一覧に飛びます。
令和3年測量士補試験の解説→令和3年測量士補試験第1問の解説記事に飛びます。
令和2年測量士補試験の解説→令和2年測量士補試験第1問の解説記事に飛びます。
測量士補試験におすすめのテキストについて→過去の記事に飛びます。
コメント